Угол естественного откоса песка: Угол естественного откоса глины. Определение угла естественного откоса грунтов
Угол естественного откоса песка. Определение угла естественного откоса песчаного грунта Определение угла естественного откоса
Лабораторная работа 1. Определение величины угла ссыпания и угла естественного откоса зернисто-кускового материала
Цель работы. Определить величины угла естественного откоса и угла ссыпания зернисто-кускового материала.
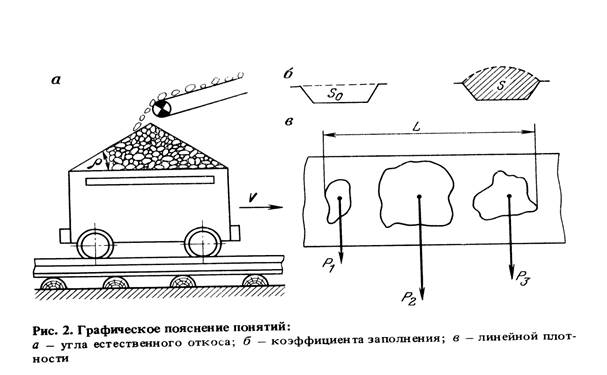
Теоретические положения . Зернисто-кусковой материал, лежащий на наклонной плоскости (например, на наклонной плоскости бункера , на наклонном ленточном транспортере и т. д.), при определенном угле наклона этой плоскости к горизонту начинает ссыпаться по ней. Такой предельный угол наклона называется углом ссыпания.
В зависимости от формы кусочков можно наблюдать два вида движения кускового материала по плоскости ссыпания: скольжение и перекатывание. Скольжение наблюдается при кусках с развитыми плоскими гранями; передвижению кусков здесь препятствует трение скольжения между гранями кусков и плоскостью ссыпания.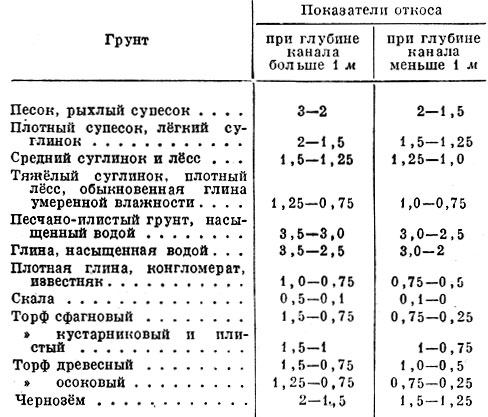
Предельное состояние покоя слоя кускового материала на наклонной плоскости имеет место тогда, когда сила трения F равна проекции М силы тяжести G на эту плоскость (рисунок 1). С другой стороны, эта же сила трения пропорциональна нормальному давлению кускового материала на наклонную плоскость
F = M = fN ,
откуда f = М / N = tgα
где f – коэффициент трения, определяемый свойствами самого материала, равный tga ;
α – угол ссыпания зернисто-кускового материала.
Рисунок 1
Если рассматривать весь слой сыпучего материала , который перемещается по гладкой наклонной плоскости, то здесь, даже в случае кусков шарообразной формы, происходит скорее скольжение материала по плоскости, чем перекатывание, так как весь материал «течет» сплошной массой.
Угол ссыпания зависит от коэффициента трения материала о плоскость ссыпания, от формы и крупности кусков, от структуры поверхности, по которой происходит ссыпание (поверхность может быть гладкой, шероховатой, ребристой и т. д.), а также он влажности самого кускового материала.
Если насыпать зернисто-кусковой материал на горизонтальную плоскость, то он располагается на ней в виде конуса. Угол между образующей этого конуса и горизонтальной плоскостью называется углом естественного откоса зернисто-кускового материала.
Угол естественного откоса всегда больше угла ссыпания (для одного и того же материала), так как наличие неровностей на поверхности материала препятствует скатыванию, а тем более скольжению кусков. Угол естественного откоса в большой степени зависит от фракционного состава кускового материала, ибо последний определяет собой общую структуру поверхности конуса. Эта разнородность размера кусков вызывает в то же время преимущественное скатывание крупных кусков материала на край насыпаемой кучи, вследствие того, что неровности поверхности оказывают меньшее сопротивление перекатыванию крупн
ых кусков, чем мелких (рисунок 2).
Тонко измельченные материалы имеют больший угол естественного откоса, т. е. меньшую сыпучесть, в связи с более развитой поверхностью трения.
Рисунок 2
Угол естественного откоса значительно зависит от влажности материала, потому что вода, располагаясь на поверхности кусков, вызывает слипание их и тем самым затрудняет движение отдельных кусков. Чем меньше куски материала, тем больше проявляется влияние влажности; но чрезмерное увлажнение приводит к увеличению послойной текучести жидкости между кусочками материала, и угол естественного откоса вновь уменьшается (таблица 1).
Таблица 1
Порода | Угол естественного откоса, град, для породы | ||
сухой | влажной | мокрой | |
Песок крупный | 30 – 35 | 32 – 40 | 25 – 27 |
Песок средний | 28 – 30 | ||
Песок мелкий | 30 – 35 | 15 – 20 | |
Гравий | 35 – 40 |
Угол естественного откоса и угол ссыпания резко уменьшаются при движении материала и плоскости, на которой он лежит. При сотрясениях или вибрациях материал интенсивно рассыпается, растекается, стремясь принять горизонтальное положение, так как при вибрациях в отдельные моменты уменьшается взаимное трение по поверхности соприкосновения кусочков друг с другом и кусочков с плоскостью. На этом основано применение вибротранспортирующих устройств, вибраторов для облегчения разгрузки бункеров, самосвалов и дозирующих устройств.
При сотрясениях или вибрациях материал интенсивно рассыпается, растекается, стремясь принять горизонтальное положение, так как при вибрациях в отдельные моменты уменьшается взаимное трение по поверхности соприкосновения кусочков друг с другом и кусочков с плоскостью. На этом основано применение вибротранспортирующих устройств, вибраторов для облегчения разгрузки бункеров, самосвалов и дозирующих устройств.
Знание углов естественного откоса и ссыпания необходимо при проектировании складских помещений, транспортеров, шахтных печей, где имеют дело с сыпучими материалами. Невозможность учета теоретически всех факторов, определяющих величину этих углов, приводит к необходимости экспериментального их определения.
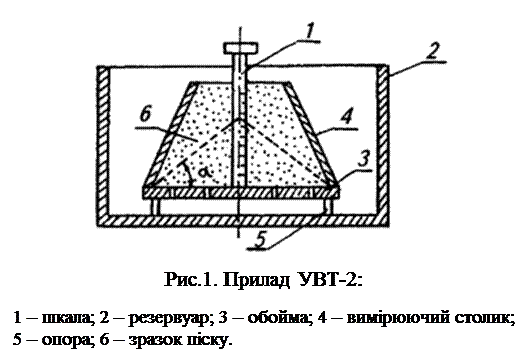
Описание установки. Для определения угла естественного откоса используется гладкая горизонтальная плоскость с нанесенными на ней делениями в сантиметрах и короткий металлический цилиндр; для определения угла ссыпания – прибор, состоящий из вала 1, на который навертывается шнур, кронштейна 2, через который шнур соединяется с подъемной доской 3, и угломера 4,
установленного у оси вращения подъемной доски. Подъемная доска снабжена указателем, показывающим на угломере угол ее подъема (рисунок 3). Для сбора ссыпавшейся массы поставлен ящик. В работе используется также линейка, весы и прямоугольная металлическая рамка.
Подъемная доска снабжена указателем, показывающим на угломере угол ее подъема (рисунок 3). Для сбора ссыпавшейся массы поставлен ящик. В работе используется также линейка, весы и прямоугольная металлическая рамка.
Рисунок 3
Проведение опыта и запись наблюдений. При определении углов естественного откоса и ссыпания используется сыпучий материал двух или трех сортов крупности.
А. Определение угла естественного откоса
1. Установить металлический цилиндр в центре горизонтальной плоскости,
2. Набрать совком сыпучий материал и высыпать его в цилиндр.
3. Медленно поднять цилиндр, предоставив материалу свободно рассыпаться по плоскости.
Б. Определение угла ссыпания
1. Уложить на подъемной доске прямоугольную металлическую рамку и полностью засыпать ее сыпучим материалом.
2. Снять прямоугольную рамку и, медленно вращая вал, привести подъемную доску в наклонное положение.
3. Когда материал начнет ссыпаться, прекратить подъем доски и записать угол ее наклона. Перенести весь материал с подъемной доски и ее подставки на лист бумаги, взвесить материал, добавить определенное количество воды (заданное преподавателем), тщательно перемешать и произвести с влажным материалом те же определения (этапы А, 1 – 4 и Б,
Когда материал начнет ссыпаться, прекратить подъем доски и записать угол ее наклона. Перенести весь материал с подъемной доски и ее подставки на лист бумаги, взвесить материал, добавить определенное количество воды (заданное преподавателем), тщательно перемешать и произвести с влажным материалом те же определения (этапы А, 1 – 4 и Б,
Результаты опытов внести в таблицу 2.
Таблица 2
Наименование исследуемого материала | Угол естественного откоса | Угол ссыпания | ||||||||
сухой материал | влажный материал | Сухой материал | Влажный материал | |||||||
tg α | tg α | |||||||||
Обработка результатов опыта.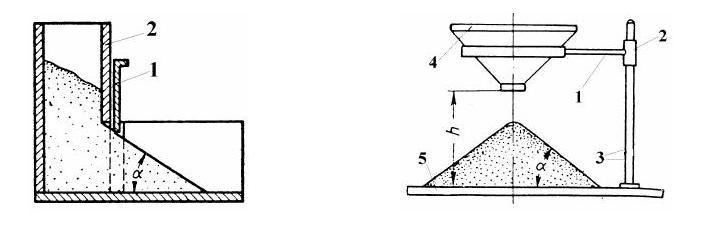 Пользуясь соотношением определить величину
tg
α
и по таблицам найти соответствующее значение α.
Пользуясь соотношением определить величину
tg
α
и по таблицам найти соответствующее значение α.
font-size:14.0pt; font-family:” times new roman>где α – угол естественного откоса, град.;
Н – высота насыпанной кучи материала, см;
D – диаметр насыпанной кучи материала, см;
font-size:14.0pt; font-family:” times new roman>– радиус насыпанной кучи материала, см,
1) Краткое изложение теории и цель работы.
2) Схема установки.
3) Таблица 2.
4) Вывод по работе.
Задание на подготовку к лабораторной работе .
1) Измельчение твёрдых материалов и их классификация .
2) Измельчение, грохочение и дозирование твёрдых тел .
Контрольные вопросы .
1) Объясните понятие «угол ссыпания».
2) Виды движения кускового материала по плоскости ссыпания.
3) Назовите факторы, от которых зависит величина угла ссыпания зернисто-кускового материала.
4) Объясните понятие «угол естественного откоса зернисто-кускового материала».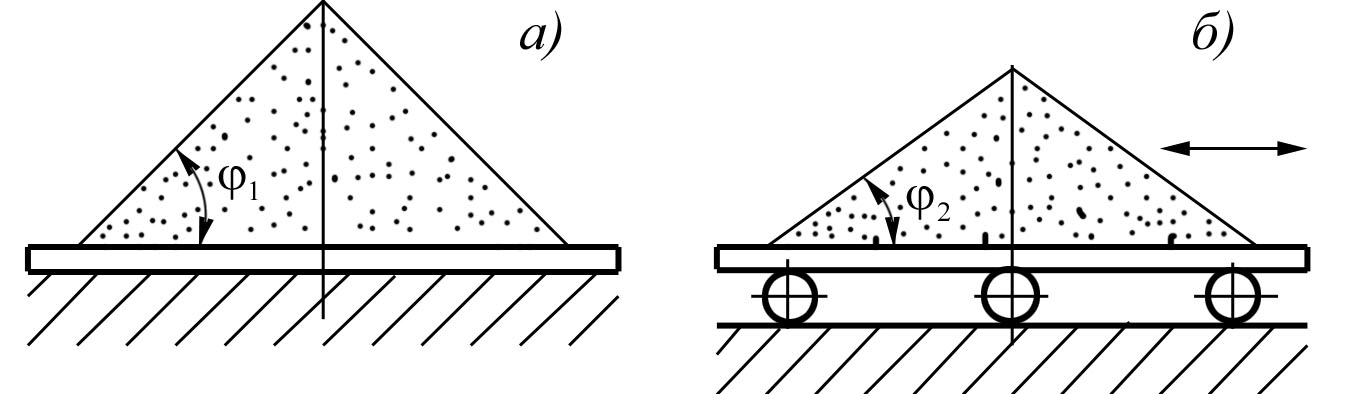
5) Назовите факторы, от которых зависит величина угла естественного откоса.
6) Скажите какая величина больше – угол ссыпания или угол естественного откоса, объясните почему.
7) Как изменяется величина угла ссыпания и угла естественного откоса при движении материала и плоскости, на которой он лежит?
8) Как угол естественного откоса зависит от влажности?
9) тонко или крупно измельчённый материал имеет больший угол естественного откоса?
10) Для чего необходимо знание углов естественного откоса и ссыпания?
Угол
естественного откоса или угол покоя – это угол между плоскостью основания
штабеля и образующей, который зависит
от рода и кондиционного состояния груза.Угол естественного откоса –
максимальный угол наклона откоса
гранулированного материала, не обладающего
сцеплением, т. е. свободно текучего
материала. Рыхлые и пористые навалочные
грузы имеют больший угол покоя, чем
твердые кусковые грузы. С увеличением
влажности угол покоя растет. При длительном
хранении многих навалочных грузов угол
покоя за счет уплотнения и слеживаемости
возрастает. Различают угол естественного
откоса в покое и в движении. В покое угол
естественного откоса на 10 – 18° больше,
чем в движении (например, на ленте
транспортера).
При длительном
хранении многих навалочных грузов угол
покоя за счет уплотнения и слеживаемости
возрастает. Различают угол естественного
откоса в покое и в движении. В покое угол
естественного откоса на 10 – 18° больше,
чем в движении (например, на ленте
транспортера).
Величина угла естественного откоса груза зависит от формы, размера, шероховатости и однородности грузовых
частиц, влажности массы груза, способа его отсыпки, исходного состояния и материала опорной поверхности.
Применяются различные методы определения величины угла естественного откоса; к числу наиболее распространенных относятся способы насыпки и обрушения.
Экспериментальное
определение сопротивления сдвигу и
основных параметров груза производится
обычно методами прямого среза, одноосного
и трехосного сжатия. Испытания свойств
груза методами прямого среза применимы
как к идеальным, так и к связным сыпучим
телам. Метод испытания на одноосное
(простое) сжатие – раздавливание применим
только для оценки общего сопротивления
сдвигу связных сыпучих тел при условном
допущении, что во всех точках испытываемого
образца сохраняется однородное
напряженное состояние. Наиболее надежные
результаты испытаний характеристик
связного сыпучего тела дает метод
трехосного сжатия, позволяющий исследовать
прочность образца груза при всестороннем
сжатии.
Наиболее надежные
результаты испытаний характеристик
связного сыпучего тела дает метод
трехосного сжатия, позволяющий исследовать
прочность образца груза при всестороннем
сжатии.
Определение угла естественного откоса мелкозернистых веществ (размеры частиц менее 10 мм) производится с помощью «наклонного ящика». Угол естественного откоса в этом случае – угол, образованный горизонтальной плоскостью и верхней кромкой испытательного ящика в тот момент, когда только начнется массовое осыпание вещества в ящике
Судовой метод определения угла естественного откоса вещества используют при отсутствии «наклоняемого ящи-
ка». В этом случае угол естественного откоса – это угол между образующей конуса груза и горизонтальной
плоскостью.
Угол естественного откоса. Способы определения в натурных условиях
Угол
естественного откоса или угол
покоя – э то
угол между плоскостью основания штабеля
и образующей, который зависит от рода
и кондиционного состояния груза. Угол
естественного откоса – максимальный
угол наклона откоса гранулированного
материала, не обладающего сцеплением,
т. е. свободно текучего материала.
Угол
естественного откоса – максимальный
угол наклона откоса гранулированного
материала, не обладающего сцеплением,
т. е. свободно текучего материала.
На практике данными о величине угла естественного откоса пользуются при определении площади штабелирования груза, количества груза в штабеле, объема внутритрюмных штивочных работ, при подсчете величин давления груза на ограждающие его стенки
Применяются различные методы определения величины угла естественного откоса; к числу наиболее распространенных относятся способы насыпки и обрушения .
Экспериментальное определение сопротивления сдвигу и основных параметров груза производится обычно методами прямого среза , одноосного и трехосного сжатия .
Определение
угла естественного откоса мелкозернистых
веществ (размеры
частиц менее 10 мм) производится с помощью
«наклонного
ящика ».
Угол естественного откоса в этом случае
– угол, образованный горизонтальной
плоскостью и верхней кромкой испытательного
ящика в тот момент, когда только начнется
массовое осыпание вещества в ящике.
Судовой метод определения угла естественного откоса вещества используют при отсутствии «наклоняемого ящика». В этом случае угол естественного откоса – это угол между образующей конуса груза и горизонтальной плоскостью.
Практика производства замеров углов естественного откоса в натурных условиях показывает, что их величина несколько изменяется в зависимости от метода отсыпки груза (струей или дождем), массы исследуемого груза, высоты , с которой производится экспериментальная отсыпка.
Для быстрых измерений удобен способ Мооса , при котором зерно насыпают в прямоугольный ящик со стеклянными стенками размерами 100х200х300 мм на 1/3 его высоты. Ящик осторожно поворачивают на 90° и измеряют, угол между поверхностью зерна и горизонтальной (после поворота) стенкой.
Общие положения
Назначение и виды земляных сооружений
Объем земляных работ очень большой, он имеется при строительстве любого здания и сооружения. Из общей трудоемкости в строительстве земляные работы составляют 10%.
Из общей трудоемкости в строительстве земляные работы составляют 10%.
Различаются следующие основные виды земляных сооружений :
Планировка площадки;
Котлованы и траншеи;
Земляные полотна дорог;
Плотины;
Каналы и др.
Земляные сооружения делятся на :
Постоянные;
Временные.
К постоянным относятся котлованы, траншеи, насыпи, выемки.
К постоянным земляным сооружениям предъявляются требования :
Должно быть прочным, т.е. сопротивляться временным и постоянным нагрузкам;
Устойчивым;
Хорошо сопротивляться атмосферным влияниям;
Хорошо сопротивляться размывающим действиям;
Должны обладать безосадочностью.
Основные строительные свойства и классификация грунтов
Грунтом называют породы, залегающие в верхних слоях земной коры. К ним относятся: растительный грунт, песок, супесь, гравий, глина, суглинок лессовидный, торф, различные скальные грунты и плывуны.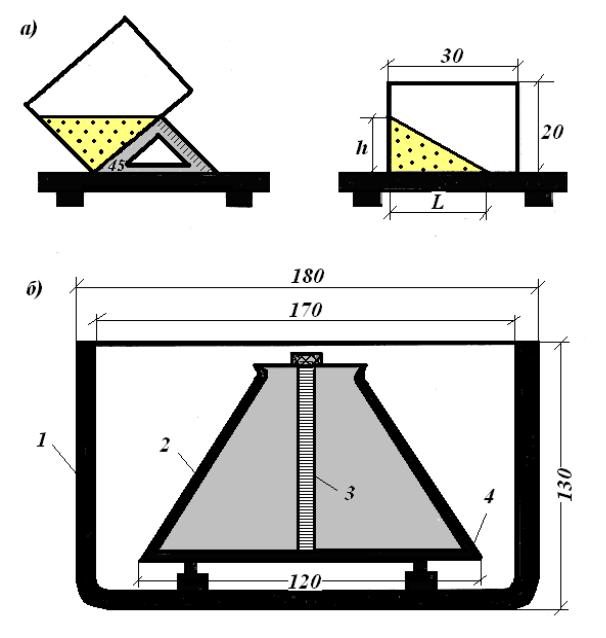
По крупности минеральных частиц и их взаимной связи различают следующие грунты :
Связные – глинистые;
Несвязные – песчаные и сыпучие (в сухом состоянии), крупнообломочные несцементированные грунты содержащие более 50% (по массе) обломков кристаллических пород размером более 2 мм;
Скальные – изверженные, метаморфические и осадочные породы с жесткой связью между зернами.
К основным свойствам грунтов, влияющим на технологию производства, трудоемкость и стоимость земляных работ относятся :
Объемная масса;
Влажность;
Размываемость
Сцепление;
Разрыхленность;
Угол естественного откоса;
Объемной массой называется масса 1 м3 грунта в естественном состоянии в плотном теле.
Объемная масса песчаных и глинистых грунтов 1,5 – 2 т/м3, скальных не разрыхленных до 3 т/м3.
Влажность – степень насыщения пор грунта водой
g b – g c – масса грунта до и после сушки.
При влажности до 5% – грунты называются сухие. При влажности от 5 до 15% – грунты называются маловлажными. При влажности от 15 до 30% – грунты называются влажные.
При влажности более 30% – грунты называются мокрые.
Сцепление – начальное сопротивление грунта сдвигу.
Сила сцепления грунтов : – песчаных грунтов 0,03 – 0,05 МП- глинистых грунтов 0,05 – 0,3 МП- полускальных грунтов 0,3 – 4 МПа- скальных более 4 МПа.
В мерзлых грунтах сила сцепления значительно больше.
Разрыхляемость – это способность грунта увеличиваться в объеме при разработке, вследствие потери связи между частицами. Увеличение объема грунта характеризуется коэффициентом разрыхления К р. После уплотнения разрыхленного грунта называется остаточной разрыхленностью К ор.
Угол естественного откоса характеризуется физическими свойствами грунта. Величина угла естественного откоса зависит от угла внутреннего трения, силы сцепления и давления вышележащих слоев. При отсутствии сил сцепления предельный угол естественного откоса равен углу внутреннего трения. Крутизна откоса зависит от угла естественного откоса. Крутизна откосов выемок и насыпей характеризуется отношением высоты к заложению m – коэффициент откоса.
При отсутствии сил сцепления предельный угол естественного откоса равен углу внутреннего трения. Крутизна откоса зависит от угла естественного откоса. Крутизна откосов выемок и насыпей характеризуется отношением высоты к заложению m – коэффициент откоса.
Углы естественного откоса грунтов и отношение высоты откоса к заложению
| Грунты | Значение углов естественного откоса и отношений высоты откоса к его заложению при различной влажности грунтов | |||||
| Сухой | Влажный | Мокрый | ||||
| Угол в град | Угол в град | Отношение высоты к заложению | Угол в град | Отношение высоты к заложению | ||
| Глина | 1: 1 | 1: 1,5 | 1: 3,75 | |||
| Суглинок средний | 1: 0,75 | 1: 1,25 | 1: 1,75 | |||
| Суглинок легкий | 1: 1,25 | 1: 1,75 | 1: 2,75 | |||
| Песок мелкозернистый | 1: 2,25 | 1: 1,75 | 1: 2,75 | |||
| Песок среднезернистый | 1: 2 | 1: 1,5 | 1: 2,25 | |||
| Песок крупнозернистый | 1: 1,75 | 1: 1,6 | 1: 2 | |||
| Растительный грунт | 1: 1,25 | 1: 1,5 | 1: 2,25 | |||
| Насыпной грунт | 1: 1,5 | 1: 1 | 1: 2 | |||
| Гравий | 1: 1,25 | 1: 1,25 | 1: 1,5 | |||
| Галька | 1: 1,5 | 1: 1 | 1: 2,25 |
Размываемость грунта – унос частиц текучей водой. Для мелких песков наибольшая скорость воды не должна превышать 0,5-0,6 м/сек, для крупных песков 1-2 м/сек, для глинистых грунтов 1,5 м/сек.
Для мелких песков наибольшая скорость воды не должна превышать 0,5-0,6 м/сек, для крупных песков 1-2 м/сек, для глинистых грунтов 1,5 м/сек.
Угол естественного откоса – это наибольший угол, который может быть образован откосом свободно насыпанного грунта в состоянии равновесия с горизонтальной плоскостью.
Угол естественного откоса зависит от гранулометрического состава и формы
частиц. С уменьшением размера зерен угол естественного откоса становится
положе.
В воздушно-сухом состоянии угол естественного откоса песчаного грунта
равен 30-40°, под водой – 24-33°. Для грунтов, не обладающих сцеплением
(сыпучих), угол естественного откоса не превышает угла внутреннего трения
Для определения угла естественного откоса песчаного грунта в воздушно-сухом состоянии используют прибор УВТ (рис. 9.11, 9.12 ), под водой – ВИА (рис. 9.13 ).
Согласно рис. 9.12 при наклоне ящика песок осыпается и, разрыхляясь, образует откос с углом, который можно определить транспортиром или по формуле
Понятие об угле естественного откоса относится только к
сухим сыпучим грунтам, а для связных глинистых оно теряет всякий смысл, так как
у последних он зависит от влажности, высоты откоса и величины пригрузки на откос
и может изменяться от 0 до 90°.
Рис. 9.11. Прибор УВТ-2: 1 – шкала; 2 – резервуар; 3 – мерительный столик; 4 – обойма; 5 – опора; 6 – образец песка
Рис. 9.12. Определение угла естественного откоса вращением емкости (а) и медленным снятием пластинки (б): А – ось вращения емкости
Рис. 9.13. Прибор ВИА: 1 – ящик ВИА; 2 – образец песка; 3 – емкость с водой; 4 – транспортир; 5 – ось вращения; 6- пьезометр; 7- штатив
При разработке и усадке разрыхленного грунта выемки и насыпи образуют естественные откосы различной крутизны. Наибольшую крутизну плоских откосов земляных сооружений, траншей и котлованов, устраиваемых без креплений, следует принимать согласно табл. 9.2. При обеспечении естественной крутизны откосов обеспечивается устойчивость земляных насыпей и выемок.
Таблица 9.2. Наибольшая крутизна откосов траншей и котлованов, град.
| 1,5 | 3,0 | 5,0 | |
| Насыпные неуплотненные | 56(1:0,67) | 45(1:1) | 38(1:1,25) |
| Песчаные и гравийные влажные | 63(1:0,5) | 45(1:1) | 45(1:1) |
| Глинистые: | |||
| супесь | 76(1:0,25) | 56(1:0,67) | 50(1:0,85) |
| суглинок | 90(1:0) | 63(1:0,5) | 53 (1:0,75) |
| глина | 90(1:0) | 76(1:0,25) | 63(1:0,5) |
| Лессы и лессовидные сухие | 90(1:0) | 63(1:0,5) | 63(1:0,6) |
| Моренные: | |||
| песчаные, супесчаные | 76(1:0,25) | 60(1:0,57) | 53 (1:0,75) |
| суглинистые | 78(1:0,2) | 63(1:0,5) | 57(1:0,65) |
Откосы насыпей постоянных сооружений выполняют более пологими, чем откосы
выемок.
Лабораторная работа №1
Определение гранулометрического состава песка и степени его однородности
Цель работы: определение свойств грунта (песка) по его гранулометрическому составу. Зная его состав и содержание в нем определения фракций, можно судить о его свойствах и применении в практике строительства (растворы, песчаные подушки, фундаменты и т.п.).
Задачи работы : получить навыки определения процентного содержания каждой фракции, квартования, определения однородности и неоднородности грунтов по графику.
Обеспечивающие средства: сита, электронные весы, навеска воздушно-сухого песка.
| Наименование определений | Размер фракции | Сумма весов фракций | Потеря | |||||
| > 2,0 | 1,0 | 0,5 | 0,25 | 0,1 | ||||
| Вес фракции, г (1 отвес) | ||||||||
| Вес фракции, г (2 отвес) | ||||||||
| Вес фракции, г (3 отвес) | ||||||||
| Вес фракции, г (среднее значение) | ||||||||
| % от общего количества | ||||||||
| Сумма % менее данного диаметра |
U = d60/d10 = 0,35/0,14 = 2,5 ≤ 3
Заключение (вывод): Так как U
Исполнители:Сельков Д. М., Старченко В.П., Яковлева Н.В.
М., Старченко В.П., Яковлева Н.В.
Лабораторная работа №2
Определение угла естественного откоса песчаного грунта в сухом и влажном состоянии
Цель работы: исследовать зависимость изменения величины угла естественного откоса песка от его влажности.
Задачи работы : получить навыки работы с прибором Литвинова, научиться правильному взятию отсчетов и определению угла естественного откоса в градусах.
Обеспечивающие средства: прибор системы Литвинова, совок, сосуд с водой, песчаный грунт.
Таблица определения угла естественного откоса
Заключение (вывод):
Угол естественного откоса, угол внутреннего трения (в механике грунтов)- угол, образованный свободной поверхностью рыхлой горной массы или иного сыпучего вещества с горизонтальной плоскостью. Иногда может быть использован термин «угол внешнего трения».
Частицы вещества, находящиеся на свободной поверхности насыпи, испытывают состояние предельного (критического) равновесия. Угол естественного откоса связан с коэффициентом трения и зависит от шероховатости зёрен, степени их увлажнения, гранулометрического состава и формы, а также от удельного веса материала.
Угол естественного откоса связан с коэффициентом трения и зависит от шероховатости зёрен, степени их увлажнения, гранулометрического состава и формы, а также от удельного веса материала.
Угол естественного откоса грунта является параметром прочности почв, и он используется для описания сопротивления трения при сдвиге почвы вместе с нормальным эффективным напряжением.
По углам естественного откоса определяются максимально допустимые углы откосов уступов и бортов карьеров, насыпей, отвалов и штабелей.
При разработке (резании) грунты разрыхляются, структура их нарушается, и они теряют связность. Также изменяются силы трения и сцепления, уменьшаясь с увеличением влажности. Поэтому устойчивость незакрепленных откосов также непостоянна и сохраняется временно до изменения физико-химических свойств грунта, связанного в основном с атмосферными осадками в летнее время и последующим увеличением влажности грунта. Так, угол естественного откоса φ для песка сухого 25…30°, песка влажного 20°, глины сухой 45° и глины влажной 15°.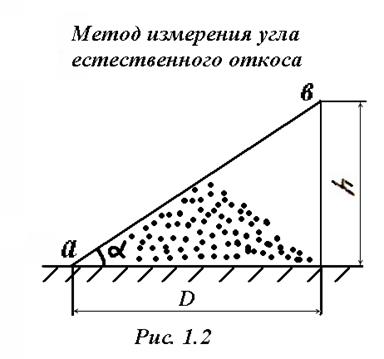 Установление безопасной высоты уступа и угла откоса является важной задачей. От правильного выбора угла откоса зависит безопасность разработки котлована, карьера.
Установление безопасной высоты уступа и угла откоса является важной задачей. От правильного выбора угла откоса зависит безопасность разработки котлована, карьера.
Исполнители:Мелехин С.А., Морохин А.В.
РСН 51-84 Инженерные изыскания для строительства. Производство лабораторных исследований физико-механических свойств грунтов
РЕСПУБЛИКАНСКИЕ СТРОИТЕЛЬНЫЕ НОРМЫ
ИНЖЕНЕРНЫЕ ИЗЫСКАНИЯ ДЛЯ СТРОИТЕЛЬСТВА.
ПРОИЗВОДСТВО ЛАБОРАТОРНЫХ ИССЛЕДОВАНИЙ
ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВ ГРУНТОВ
РСН 51-84
Госстрой РСФСР
ГОСУДАРСТВЕННЫЙ КОМИТЕТ РСФСР ПО ДЕЛАМ
СТРОИТЕЛЬСТВА
СОДЕРЖАНИЕ
|
1. 2. ОРГАНИЗАЦИЯ ЛАБОРАТОРНЫХ РАБОТ . 2 3. ОБОРУ Д ОВАНИЕ, ПРИБОРЫ, ПОМЕЩЕНИЯ .. 2 4. ХРАНЕНИЕ, ТРАНСПОРТИРОВАНИЕ И ПОДГОТОВКА К АНАЛИЗАМ ОБРАЗЦОВ ГРУНТОВ .. 3 5. МЕТОДЫ ИССЛЕДОВАНИЯ ГРУНТОВ .. 3 6. ЛАБОРАТОРНАЯ ДОКУМЕНТАЦИЯ .. 4 Приложение 1 . 4 Рекомендуемое . 4 Приложение 2 . 5 Рекомендуемое . 5 Приложение 3 . 6 Рекомендуемое . 6 Приложение 4 . 6 Рекомендуемое . 6 Приложение 5 . 6 Рекомендуемое . 6 Приложение 6 . 7 Рекомендуемое . 7 Приложение 7 . 8 Рекомендуемое . 8 Приложение 8 . 8 Рекомендуемое . 8 Приложение 9 . Рекомендуемое . 9 Приложение 10 . 10 Приложение 11 . 11 Приложение 12 . 12 |
Разработаны трестами инженерно-строительных изысканий МосЦТИСИЗ, УралТИСИЗ, ТулаТИСИЗ Производственного объединения по инженерно-строительным изысканиям («Стройизыскания») Госстроя РСФСР.
Исполнители: И.Н. Шишелов, канд. тех. наук Ю.В. Сырокомский, И.Б. Когос, Т.Д. Белоглазова, Р.А. Меньшикова, Л.И. Подкорытова, А.С. Романова.
Внесены и подготовлены к утверждению Производственным объединением по инженерно-строительным изысканиям («Стройизыскания») Госстроя РСФСР.
Вводятся впервые.
|
Государственный комитет РСФСР по делам строительства (Госстрой РСФСР) |
Республиканские строительные нормы |
РСН 51-84 Госстрой РСФСР |
|
Инженерные изыскания для
строительства. |
Вводятся впервые |
Настоящие Республиканские строительные нормы распространяются на организации, выполняющие исследования грунтов при инженерных изысканиях для строительства объектов промышленного, жилищно-гражданского и сельскохозяйственного назначения и устанавливают основные требования к производству лабораторных исследований физико-механических свойств грунтов.
1.1. Лабораторные исследования грунтов следует выполнять в соответствии с требованиями государственных стандартов, строительных норм и правил, а также настоящих Республиканских строительных норм.
|
Внесены Производственным объединением по инженерно-строительным изысканиям («Стройизыскания») Госстроя РСФСР |
Утверждены постановлением Государственного
комитета РСФСР по делам строительства от 15 июня 1984 г. |
Срок введения в действие 1 января 1985 г. |
1.2. Состав лабораторных исследований грунтов должен устанавливаться в соответствии с требованиями действующих нормативных документов и программ на производство изыскательских работ.
1.3. Лабораторные исследования грунтов должны выполняться с применением прогрессивных методов, современных приборов и оборудования, обеспечивающих высокое качество испытаний грунтов, наибольшую производительность труда и сокращение продолжительности лабораторных работ.
1.4. При производстве лабораторных исследований грунтов следует осуществлять мероприятия по экономии материалов и электроэнергии, а также обеспечивать бережное отношение к оборудованию, приборам, инструменту и инвентарю.
1.5. Стоимость лабораторных
работ определяется согласно Сборнику цен на изыскательские работы для
капитального строительства.
1.6. При производстве лабораторных работ необходимо выполнять требования, предусмотренные правилами и инструкциями по охране труда и технике безопасности.
2.1. Лабораторные работы следует проводить в соответствии с планом-графиком и заданиями на их выполнение.
План-график составляется начальником лаборатории и согласовывается с начальником инженерно-геологических производственных подразделений – заказчиками лабораторных исследований грунтов.
Зад ание на л абораторные и сследования грунтов состав ляется подразделением-заказчиком эт их работ. Зада ние должно быть подп исано н ачаль ником подр азделения и главным гео лого м производственного подра зделе ния-заказчнка.
2.2. Контроль качества
лабораторных исследова ний грунтов – вхо дн ой, операционный,
приемочный – следу ет осу ществлять в соответст вии
со станд артом предприятия
комплексной с истемы упр авлен ия качеством
инжен ерных изысканий
в строительстве (КС УКИИС)
на всех стад иях работ.
Входному ко нтролю следует подвергать образцы грунта, поступающие на исследования, задан ия заказчика, вновь поступающ ие оборудование, пр иборы, инструменты. Входной контроль должен быть сплошным и осуществляться началь ником лаборатор ии или специ аль но уполномоченным работником.
Операц ио нный контроль следует провод ить в процессе прои зводства лабораторных исс ледований грунтов и ведения перв ичной документа ции. Особому контролю подлежат сл едующие рабоч ие процессы: отбор средней пробы, вырезка обра зцов грунта, п оддержание темп ературы пр и определенной влажности, периодическая тар ировка ар еометра при определении гранулометрического состава, подсч ет нагрузок пр и определении сопрот ивления сре зу.
Оп ерац ионный контроль пр иборов
следует проводить в соответствии
с требованиями приложения 1. Ис по лн ители ра бот долж ны проводить сплошной операционный
контро ль (самоко нтроль),
н ач альник лаборатории ил и спец иально
уполномоченный работник – выбороч ный.
При емоч ному контролю следу ет подв ергать результат ы лабораторных иссл едований грунтов, подготовленн ые к передаче заказч ику. При емочный ко нтрол ь долже н 6ыть спло шным и осуществл яться начальником лаборатории.
2.3. Ре зу льтаты лабораторных исследован ий грунтов выдаются зака зчик ам в виде машинно-ориентированных ведомостей приобр аботке данных на ЭВМ или в виде ведомостей паспортов ре зультатов и сследований грунтов.
2.4. Информ ацию об отклонениях от стандартов при прове дении лабораторных исследований грунтов начальник лабор атории не медленно передает заказчику лабораторных работ.
3. 1. Лаборатор ии исс ле дован ия грунто в должны быть обеспечены оборудо ванием, приборами, инструментом и и нвентарем в соотв етств ии с Таб елям и ос нащен ия изыскательских и п роектно-изыскательских
организаций пр иборами, оборудовани ем, транспортными средствами, ла герным снаряж ением и средствами свя зи.
3.2. Для метролог ического обеспечен и я производства л абор аторных исследований фи зико-мех анических свойст в грунтов оборудование и прибор ы грунтовой лаборатории должны подвергаться пров ерк е в установл енные сроки в соответствии с тр ебованиями ГОСТ 8.002-71 и стандартов п редприятия КС УКИИС.
3.3. Д ля об еспеч ен ия постоянной эксплуат ационной готовности оборудования и приборов с ледует применять с истему планово – предупредительных ремонтов, предусматривающую проведение компл екса предупредительных м ер опр иятий, направленных на устранен ие прогрессирующих и зносов.
3 .4
. Техническо е обслуж ивание,
предусматривающее на дзор,
уход, про верку
сост ояния оборудования
и приборов, за исключением
электрооборудования, должно проводиться co гласно го довому плану-графику
п ерсоналом г py нтовой лаборатории – препараторами, лаборантами, техниками,
инженера ми.
3 .5. Текущий ре монт обору дова ния и приборо в, предусматривающ ий замену или восстано вление дет ал ей и узлов, операции, устраняю щие неисправности, и т ехн ическое обслуж ивание электрооборудования должны про водиться ремонтно-механической службой изыскате льско й организац ии.
3.6. В помещен иях лаборатории иссле дования грунтов оборудование сле дует группировать исходя и з необхо димости его совместной работы, а также по принц ипу одинакового в оздействия на окружающую среду (выделение пыли, тепла, паро в; шум и т.п.) и воздействия окружающей среды (вибрация, температура, влажность).
3.7. Состав помещен ий лаборатор ии иссл едова ния грунтов устанавли вают в зависимости от состава, свойств, состояния грунтов; состава и кол ичества оборудования. М инимальный и максимальный составы помещений приведены в приложении 2.
3.6. Последовательность
распо ложения помещен ий
устанавливают согласно мар шрутам движени я грунтов по анализам.
3.9. Площадь помещ ений устанавливают в зависимости от состава и количества обору дования, размеров прохо дов между оборудованием, количества сотрудн иков.
3.10. Особые требования к пл аниро вке лабораторий и сследован ий грунтов пр ив еде ны в приложении 3.
3.11. Особые требования к водоснабжению, кан ал изац ии, вентиляции, электроснабжению л абор атори и исследования грунтов пр иведены в приложении 4.
4.1. Приемку и хр ан ение образцов грунтов в лаб оратор ии исследования грунтов следует производить в соответствии с требов ан иям и ГОСТ 12071-72.
Подразделению-заказчику с ледует д оставлять и раскладывать на полки хран ил ища лаборатории образцы в том порядке, в котором он и в несены в задание.
Н ача льн ику лаборатори и или с пециально уполномоченному работнику
в пр исутстви и
геолог а, в едущего
объ ект, следует проверять
сохра нность обра зцо в, отсутствие механических
повреждений уп аковк и, д остаточность и приг одность обра зцов
для производства, предусмотренного заданием состава
определений.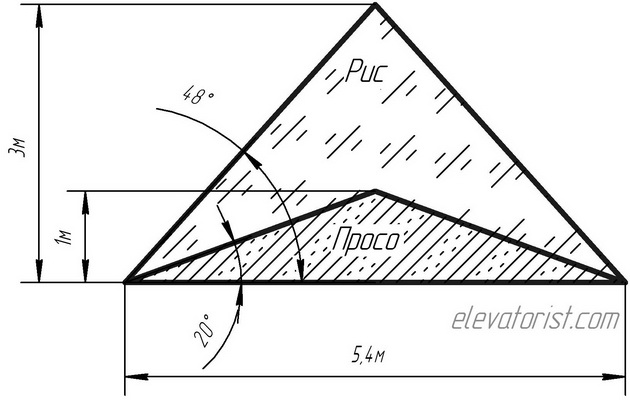
4.2. Горизонтальное транспортирование гру нта в помещении л аборатории следует осу ществ лять с помо щью ру чных тра нспорт ных тел ежек, верт икаль ное – гру зовыми ли фт ам и или специальными подъемниками.
4.3. Исследование физико-механических свойств грунтов при вскрыт ии образцов следует н ач инать с визуального и зучения и описания обра зцов. Описание должно содержать сведения о сост аве , литологических особ ен ност ях и состоянии образцов.
4.4. Вырезку обр азцов и по дготовку грунтов к анализам следует производить, как правило, с помощью механизмов.
5.1. Классификацию грунтов следует проводить в соответствии с требованиями ГОСТ 25100-82.
5.2. Гранулометрический и микроагрегатный состав следует определять в соответствии с т ребованиями
ГОСТ
12536-79. Просеивание грунтов следует производить
с помощь ю
механических с и т, взбалтывание – с помощью механического взбалтывателя .
5.3 . Пло тн ость следует определять в соответствии с требованиями ГОСТ 5180 -75.
5.4. Плотность грунта следует определять в соответствии с требованиями ГОСТ 5182-78. Плотность грунта в рыхлом и плотном состоянии следует определять в соответствии с требованиями приложения 5.
5.5.Плотность частиц грунта следует определять в соответствии с требованиями ГОСТ 5181-78.
5.6.Плотность частиц скального грунта следует определять в соответствии с требованиями приложения 6.
5.7.Границы текучести и раскатывания следует определять в соответствии с требованиями ГОСТ 5183-77.
5.8..При определении границы текучести следует применять механизированные способы опускания конуса (без дополнительного усилия) и автоматизированные способы отсчетов промежутков времени опыта.
5.9.Максимальную молекулярную влагоемкость, следует определять в соответствии с требованиями приложения 7.
5.10.Характеристики набухания и усадки следует
определять в соответствии с требованиями ГОСТ
24143-80.
5.11.Размокаемость следует определять в соответствии с требованиями приложения 8.
5.12.Характеристики просадочности, следует определять в соответствии с требованиями ГОСТ 23161-78.
5.13.Удельное сопротивление пенетрации, следует определять в соответствии с требованиями приложения 9.
5.14.Максимальную плотность следует определять в соответствии с требованиями ГОСТ 22733-77. Следует применять механизированный способ поднятия груза и автоматизированный способ отключения прибора после проведения цикла ударов.
Угол естественного откоса следует определять в соответствии с требованиями приложения 10.
Коэффициент фильтрации следует определять в соответствии с требованиями ГОСТ 25584-83. Следует применять автоматизированные способы отсчета времени понижения жидкости на заданную величину.
5.17. Суффозионную сжимаемость следует определять по ГОСТ 25585-83.
5. 18. Сжимаемость следует определять
в соответствии с требованиями ГОСТ 23908-79.
18. Сжимаемость следует определять
в соответствии с требованиями ГОСТ 23908-79.
5.19. Сжимаемость элювиальных грунтов, следует определять в соответствии с требованиями приложения 11.
5.20. Сопротивление срезу следует определять в соответствии с требованиями ГОСТ 12248-78. В приборах с постоянной скоростью среза следует применять механизированные устройства перемещения каретки и автоматизированные средства фиксации максимального усилия динамометра на участке деформации образца 0-5 мм и отключения прибора при достижении деформации 5 мм.
5.21.Предел прочности скальных грунтов от пониженной до весьма низкой прочности при одноосном сжатии образцов правильной формы следует определять в соответствии с требованиями ГОСТ 17245-79.
5.22. Предел прочности
скальных грунтов от очень прочных до мало прочных при одноосном сжатии образцов
правильной фирмы следует определять в соответствии с требованиями ГОСТ
21153. 0-75* и ГОСТ
21153.2-75.
0-75* и ГОСТ
21153.2-75.
5.23. Предел прочности скальных грунтов образцов произвольной формы следует определять в соответствии с требованиями ГОСТ 21941-81.
5.24. Коэффициент выветрелости следует определять в соответствии с требованиями приложения 12.
5.25. Коррозионную активность следуют определять в соответствии с требованиями ГОСТ 9.015 -74.
5 .26. Относительное содержание растительных остатков и степени разложения заторфованных грунтов следует определять в соответствии с требованиями ГОСТ 23740-79.
6.1. Рабочи е журна лы, выхо дны е ведомости, паспорта и други е лабор аторные документы следует оформлять в соответстви и с требованиями государственных стандартов и «Пособия по составле нию и оформлен ию документа ци и инженерных и зысканий для строительства».
6.2. Тер мины и опре деления,
пр и меняемые
в л абораторной докум ентаци и, должны
соотв етствовать приведенным
в государственном стандарте.
6.3. Ед иницы ф из ических величин, на именован ие и обоз наче ние этих единиц, применяющиес я в лабораторной докум ент ации, должны соответствовать е диницам, пр иве денным в ГОСТ 8.417-81 и в СН 528-80.
ОПЕРАЦИОННЫЙ КОНТРОЛЬ ПРИБОРОВ
Настоящая методика контроля распространяется на: балансирный конус, сита, весы, компрессионные и срезные приборы, приборы предварительного уплотнения. Общим требованием контроля является внешний осмотр. Устанавливают отсутствие на деталях приборов изгибов, вмятин, зазубрин, частиц грунта. Контроль разделяется на ежесменный и ежеквартальный. Для каждого прибора в первом подпункте настоящей методики приведены требования ежесменного контроля, во втором - ежеквартального. Приборы, не удовлетворяющие требованиям методики, к применению не допускаются.
1. Балансирный конус
Острие конуса не должно быть
затуплено.
Измерьте глубиномером (штангенциркулем) расстояние от вершины до основания конуса (25 мм) с точностью 0,1 мм. Сверьте показания с полученными при введении конуса в работу. Расхождение показаний не должно превышать 0,2 мм. Конус должен быть прочно соединен с дугой, дуга – с грузами.
2. Сита для просеивания грунтов
Просмотрите сетки сит на свет. Сетки не должны иметь нарушений плетения, смещения и обрыва проволок, разрывов в местах крепления к корпусу.
Просмотрите под микроскопом с сорокакратным увеличением сита № 0,1; 0,25; 0,5 в пяти местах по радиусу сита. Отверстия по форме должны представлять квадрат. Определите размеры отверстий по шкалеокуляpa Гюйгена. Результаты не должны отличаться от номинальных более чем на 20%.
Определите размеры 5-ти отверстий в ситах №
1 и 2 по радиусу каждого сита.
Измерьте штангенциркулем пять отверстий по радиусу каждого сита № 5 и 10. Размеры
отверстий сеток не должны отличаться от номинальных более чем на 10 %.
Размеры
отверстий сеток не должны отличаться от номинальных более чем на 10 %.
Нажмите рукой последовательно на обруч, диск сверленых сит, диск днища. Детали при нажиме на них не должны качаться.
3. Весы лабораторные квадрантные
3.1. Проверьте положение воздушного пузырька уровня весов. Переведите пузырек в центр контрольной окружности, вращая ножки весов.
Совместите нулевую отметку шкалы с нулевой отметкой на экране. Поместите на чашку весов образцовую гирю, масса которой соответствует диапазону измерения массы по шкале. Операции повторяйте до достижения необходимого предела взвешивания. Разность показаний не должна превышать допустимой погрешности взвешивания.
3.2. Проверьте четкость изображения шкалы на экране, добейтесь четкости перемещением лампы освещения шкалы весов.
4. Компрессионный прибор
4.1.
При подготовке прибора к опыту просмотрите на свет днище и штамп. Все отверстия
должны пропускать свет.
Все отверстия
должны пропускать свет.
Канаты механизма сжатия должны лежать в проточенных канавках.
Верхний луч сектора рычажного устройства не должен занимать положение ниже условной горизонтальной линии, проведенной через ось рычажного устройства.
У ножек индикаторов должен оставаться ход не менее 3 мм. Ножки индикаторов не должны подходить к краю опорных пят ближе 2 мм.
Между держателем индикатора и арретиром одометра должен быть зазор не менее 3 мм.
4.2. Проверьте плотность прилегания днища к корпусу одометра. Днище должно легко вставляться в корпус и при поочередном нажиме пальцами в трех местах по краю не должно качаться.
Проверьте возможность перемещения штампа внутри одометра. Штамп, вставленный в направляющее кольцо, должен от собственной массы опускаться на днище собранного одометра.
Измерьте штангенциркулем с
точностью 0,1 мм высоту кольца в трех
местах. Расхождение между наибольшим и наименьшим измерениями должно быть не
более 0,5 мм.
Расхождение между наибольшим и наименьшим измерениями должно быть не
более 0,5 мм.
Проверьте горизонтальность панели стола прибора с помощью слесарного уровня. Проверьте равновесие рычажного устройства.
Устройство, оставленное в положении, при котором средний луч сектора примерно горизонтален, должно оставаться в этом положении.
Проверьте чувствительность рычажного устройства. Устройство из положения равновесия должно выходить от груза массой 50 г, положенного на подвеску.
5. Срезной прибор
5.1. Проверьте штамп, диск нижней сбоймы, канаты, равновесие и чувствительность рычажных устройств в соответствии с требованиями раздела 4 настоящей методики.
Соберите нижнюю часть
срезывателя. Затяните винты, крепящие днище, нижнюю обойму. Все детали должны
легко вставляться в свои места. Винты должны без применения больших усилий закреплять
детали. Нижняя часть срезывателя не должна качаться при нажиме на нее рукой.
5.2. Проверьте горизонтальность панели стола прибора с помощью слесарного уровня.
6. Прибор предварительного уплотнения
6.1. Проверьте штампы, канаты в соответствии с требованиями раздела 4 настоящей методики.
Сектор незагруженного прибора под действием собственной массы должен занимать положение, при котором подвеска не доходит до пола на 20-40 мм. Проверьте центральное расположение загруженной обоймы в ванне.
6.2. Проверьте монтируемость обоймы. Кольца не должны перемещаться в собранной незагруженной образцом грунта обойме при перевертывании ее.
Проверьте горизонтальность панели стола прибора с помощью слесарного уровня.
М ИНИМАЛЬНЫЙ И МАКСИ МАЛЬНЫЙ СОСТА ВЫ ПОМЕЩЕНИЙ ЛАБОРАТОРИИ И ССЛЕДОВАНИЯ ГРУНТОВ
Минимальны й состав
Помещение приемки и подготовки грунтов к исследованиям.
Хранилище образцов грунта.
Помещение для определения физико-механических свойств грунтов.
Помещение для определения химических свойств грунта.
Максимальный состав
Помещение приемки образцов грунта.
Хранилище образцов грунта.
Помещение подготовки грунтов к исследованиям.
Помещение для определения физических свойств грунтов.
Помещение для определения химических свойств грунтов.
Помещение для сдвиговых приборов и прессов.
Помещение для компрессионных приборов.
Помещение для дробилок, полочного барабана, гравийных сит.
Помещение для камнерезного и шлифовального станков.
Помещение обработки результатов исследований.
Грунтовый архив.
ОСОБЫЕ ТРЕБОВАНИЯ К ПЛАНИ Р ОВКЕ ЛАБОРАТО Р И Й ИССЛЕДОВАНИЯ ГРУНТОВ
При проектировании грунтовых
лабораторий следует предусматривать погрузочно-разгрузочные площадки, подъезды
и подходы к ним.
Для разгрузки, погрузки образцов и отработанного грунта у здания лаборатории следует проектировать грузовую платформу, расположенную на одном уровне с полами кузова автомашин и первого этажа лаборатории.
Лабораторию исследования грунтов следует располагать на первом этаже знания. Допускается разрывать лабораторию по этажам при наличии в здании грузового лифта или специального подъемника и располагать лабораторию в одном из этажей от цокольного этажа до верхнего при обязательном расположении помещения приемки в первом этаже. Помещения приемки и хранилища, образцов в этом случае следует размещать вблизи лифта.
Полы помещений для компрессионных, сдвиговых приборов, прессов, дробилок, полочного барабана, камнерезного станка должны быть защищены от вибрации.
В помещениях лаборатории
углы колонн, проемов, выступающие элементы конструкций должны быть защищены от
повреждений транспортными тележками.
ОСОБЫЕ ТРЕБОВАНИЯ К В О Д ОСНАБЖЕНИЮ, КАНАЛИЗАЦИИ, ВЕНТИЛЯЦИИ, ЭЛЕКТРОСНАБЖЕНИЮ ЛАБОРАТОРИЙ ИССЛЕДОВАНИЯ ГРУНТОВ
Мойки, кроме водоразборных кранов, должны быть оборудованы дополнительно специальной лабораторной арматурой: двумя кранам и холодной воды с наконечниками для присоединения шлангов, кранами со смесительным приспособлением с удлиненными отростками.
Сброс сточных жидкостей из моек грунтовой лаборатории должен производиться через местные установки для обработки сточных жидкостей.
Для вытяжных шкафов и зондов над сушильными шкафами, мельницами грунтовыми, дробилками, установками для просева грунта, гравийными ситами, полочными барабанами следует предусматривать самостоятельные вытяжные системы вентиляции с механическим побуждением.
В хранилище образцов следует
предусматривать кондиционирование и увлажнение воздуха, а в помещении компрессионных
приборов – только кондиционирование воздуха.
Электрические линии, питающие автоматические приборы и оборудование непрерывного действия, должны обладать повышенной надежностью и отключаться отдельно от общего отключающего аппарата лаборатории исследования грунтов.
МЕТОД ОПРЕ ДЕЛЕНИЯ ПЛОТ Н ОСТИ ПЕСЧ А НОГО ГРУНТА В РЫХЛОМ И ПЛОТНОМ СОСТОЯНИЯХ
Настоящая методика распространяется на песчаные грунты и устанавливает метод лабораторного определения плотности грунта в рыхлом и плотном состояниях.
1. Общие положения
1.1. Плотность грунтов в рыхлом и плотном состояниях следует определять как отношение масс грунтов в названых состояниях к их объемам.
1.2. Определение плотности песчаного грунта проводят на воздушно-сухих грунтах.
1 . 3. Взвешивания производят с точностью ± 0,01 г.
1.4. Определение
плотности грунта в каждом состоянии проводят с двух кратной повторностью.
2. Аппаратура
Весы лабораторные по ГОСТ 19491-74.
Прибор СУГ, состоящий из металлического стакана объемом 250 см 3 (внутренний диаметр 60 мм) с насадкой.
Колотушка деревянная или вибростол.
Воронка конусообразная с длинным стеблем № 7.
Сито с сеткой № 5 по ГОСТ 3584-73.
Линейка металлическая негнущаяся.
3. Подготовка к испытанию
3.1. Песчаный грунт просеивают через сито с сеткой № 5.
3 .2. Отбирают среднюю пробу песчаного грунта.
4. Проведение испытания
4.1. Взвешивают пустые, сухие стаканы.
4.2. Для получения рыхлого состояния грунта заполняют стакан песком через воронку. Стебель воронки держат на расстоянии 10-20 мм от поверхности грунта в стакане.
4.3.
Для получения плотного состояния грунта стакан заполняют песком порциями при
постоянном постукивании колотушкой о стенки стакана.
4.4. Для получения плотного состояния грунта при наличии механизма уплотнение производят на вибростоле.
4.5. Избыток грунта при полном заполнении стаканов удаляют линейкой вровень в краями стаканов.
4.6. Взвешивают стаканы с грунтом.
5. Обработка результатов.
Соответствует ГОСТ 5182-78.
МЕТОД ОПРЕДЕЛЕНИЯ ПЛОТНОСТИ ЧАСТИЦ СКАЛЬНЫХ ГРУНТОВ
Настоящая методика распространяется на скальные грунты и устанавливает метод лабораторного определения плотности частиц.
1. Общие положения
Соответствуют ГОСТ 5181-78.
2. Аппаратура
Соответствует ГОСТ 5181-78.
Добавляется ступ к а агатовая или яшмовая с пестом по ГОСТ 9147- 80* или ступка механическая СМБН.
3. Подготовка к испытанию
3.1.
Образец скального грунта массой 250-500 г
дробят молотком на твердом основании на мелкие обломки. Обломки грунта,
находящиеся в воздушно-сухом состоянии, растирают в ступке, а затем просеивают
через сито с сеткой № 2. Частицы грунта,
оставшиеся на сите, измельчают в ступке и снова просеивают.
Обломки грунта,
находящиеся в воздушно-сухом состоянии, растирают в ступке, а затем просеивают
через сито с сеткой № 2. Частицы грунта,
оставшиеся на сите, измельчают в ступке и снова просеивают.
3 .2. Отбирают среднюю пробу грунта массой 100-200 г, избегая «круглых» значений 1 00, 150 и ли 200 г.
3.3. Из тщательно перемешанной средней пробы берут навеску в стеклянный стаканчик, масса навески – из расчета не менее 15 г на каждые 100 мл вместимости пикнометра.
3.4. Навеску высушивают в сушильном шкафу до постоянной массы и охлаждают по ГОСТ 5180-75.
3.5. Допускается использовать воздушно-сухие грунты с поправкой на гигроскопическую влажность по ГОСТ 5181-78.
3 .6. Дистиллированную воду кипятят в течение 1 ч и хранят в закупоренной бутыли.
3.7. Составляют таблицу масс
пикнометров с дистиллированной водой при различных температурах. Массы
пикнометров с дистиллированной водой при различных температурах вычисляют по
ГОСТ 5181-78.
4. Проведение испытан и я
Соответствует ГОСТ 5181-78.
5. Обработка результатов
Соответствует ГОСТ 5181-78.
МЕ ТОД ОПРЕ ДЕЛЕ НИЯ МАКСИМАЛЬНОЙ МОЛЕКУЛЯРНОЙ ВЛАГОЕМКОСТИ
Настоя щая метод ика распространяется на пылевато-глинистые и п есчаные грунты и устанавли вает мето д л абораторного определ ения максимально й молекул ярной влагоемкости.
1. Общие положения
1.1. Молекулярная влагоемкость грунта – способность частиц грунта удерживать молекулярным притяжением на своей поверхности т о или иное количество волы.
1.2. Максимальную молекулярную влагоемкость, следует определять как влажность грунтовой пасты после, прессования ее до завершения водоотдачи грунта.
1.3.
Максимальную молекулярную влагоемкость пылевато-глинистых грунтов определяют на
образцах с естественной влажностью.
1.4. Определение максимальной молекулярной влагоемкости проводят с двух кратной повторностью.
2. Аппаратура
Соответствует ГОСТ 5180 – 75.
Добавляются:
пресс рычажный, винтовой или гидравлический, исключающий возможность поворота плит; шаблон металлический толщиной 2 мм с отверстием диаметром 50 мм;
пластины металлические;
чашка фарфоровая по ГОСТ 9147-73;
линейка металлическая негнущаяся;
вазелин технический;
ткань хлопчатобумажная;
бумага фильтровальная.
3. Подготовка к испытанию
Соответствует ГОСТ 5183-77.
4. Проведение испытания
4.1. На кусочек ткани кладут
шаблон, смазанный вазелином. Заполняют шаблон грунтовой пастой. Избыток пасты удаляют
линейкой, перемещаемой по поверхности шаблона. Шаблон поднимают, а полученную
лепешку покрывают вторым кусочком ткани.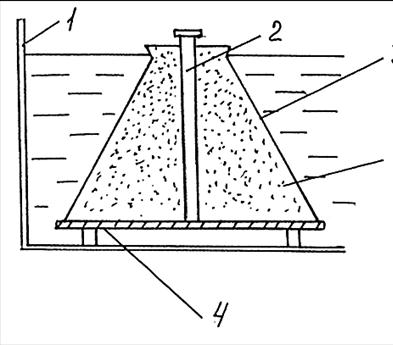
4.2. На пластину кладут стопку фильтрованной бумаги из 20 фильтров диаметром 90 мм, лепешку в ткани, такую же стопку фильтровальной бумаги, пластину.
4.3 , Полученный таким образом пакет помещают под пресс и выдерживают под постоянным давлением в 1 МПа в течение: пески и супеси – 10 мин, глины и суглинки – 30 мин. За одно прессование можно испытать несколько образцов, ограничение количества диктуется конструкцией пресса (расстояние между плитами).
4.4. Освобождают лепешку от пластин, фильтровальной бумаги, ткани. Сгибают лепешку пополам. Ломкость ее показывает, что водоотдача завершена.
4.5. Влажность образца определяют по ГОСТ 5180-75.
5. Обр аботка результатов испытания
Полученную влажность принимают за максимальную молекулярную влагоемкость.
МЕ ТО Д ОПРЕДЕЛЕНИЯ РАЗМОКАЕМОСТИ
Настоящая методика
распространяется на пылевато-глинистые грунты и устанавливает метод
лабораторного определения размокаемости.
1. Общие положения
1.1. Размокаемость – способность грунтов терять в воде связность.
1.2. Размокаемость характеризуется временем и характером размокания грунтов.
1.3. Для определения размокаемости грунтов применяют подземную воду, взятую на месте отбора образца. Допускается применение водопроводной воды.
2 . Аппаратура
Прибор ПРГ-2.
Нож.
Пресс для вырезки образцов.
Вазелин технический.
3. Подготовка к испытанию
3.1. Из монолита грунта вырезают образец кольцом – пробоотборником прибора ПРГ-2 по ГОСТ 5182 -78.
3.2. Отбирают пробу на влажность по ГОСТ 5180-78.
4. Проведение испытания
4.1. Вырезанный образец грунта ставят на сетку прибора и опускают в ванну прибора, наполненную водой.
4.2.
Наблюдают за образцом и делают записи в журнале в следующие промежутки времен и:
1; 30 мин,
1; 6;
24; 48 ч.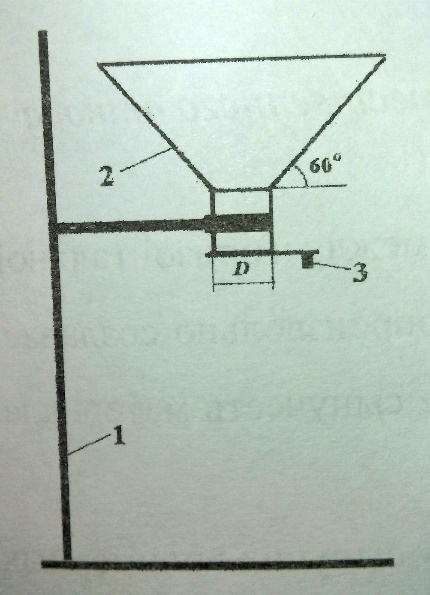
4.3. Если образец не размокнет через 48 ч, дают его описание и опыт прекращают.
5. Обработка результатов испытания
5.1. По времен и размокания образца ра зл ич ают т ипы размокаемости:
мгновен ная – по лностью з а 1 мин;
очень быстрая – более 80-90 % объема з а 30 мин;
быстрая – более 50 % объема за 1 ч,
мед ленная – менее 50 % объема за 6 ч;
очень медленная – менее 25 % объ ема за 24 ч;
не размокающий грунт – менее 10 % объ ем а за 48 ч.
5.2. По характеру размокания образца разл ич ают фор му, ра змеры (крупные, мелкие комочк и, чешуйк и, пыль) , после довательность распада.
М ЕТОД ОПРЕДЕЛЕНИЯ УДЕЛЬНОГО СОПРОТИ ВЛЕНИЯ ПЕ НЕТРАЦИИ
Настоящая методика
распространяется на пылевато-глинистые грунты и устанавливает метод лабораторного
определения удельного сопротивления пенетрации.
Методика не распространяется на пылевато-глинистые грунты, содержащие крупнообломочные включения размером более 2 мм в количестве более 10 % по массе.
1. Общие положения
1.1. Пенетрацией называется внедрение в грунт конического наконечника на глубину, не превышающую высоту конуса.
1.2. Удельное сопротивление пенетрации глинистых грунтов определяется, как отношение вертикального усилия, передаваемого на конус в килограммах, к квадрату глубины погружения конуса в сантиметрах.
1.3. Глубину погружения конуса определяют с точностью 0,1 мм.
1.4. Удельное сопротивление пенетрации определяют с точностью 0,01 кг/см2.
1.5. Пенетрацию проводят с четырехкратной повторностью (по две пенетрации на каждой стороне образца).
2. Аппаратура
Пенетрометр, состоящий из
станины со стол и ком и подвижной части, имеющей полированный конус и грузовую
площадку.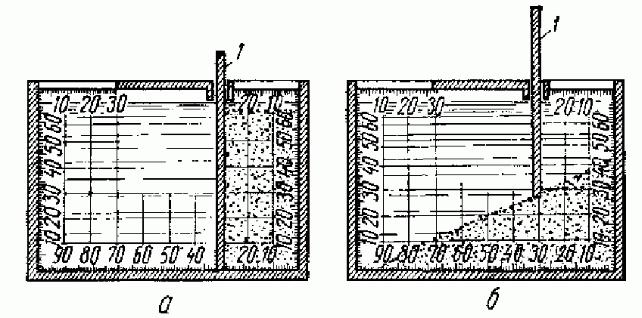 Перемещение конуса фиксирует индикатор часового типа. Конус имеет угол
раскрытия 30 ° , высоту 30-40 мм. Масса подвижной част и 150-300 г.
Перемещение конуса фиксирует индикатор часового типа. Конус имеет угол
раскрытия 30 ° , высоту 30-40 мм. Масса подвижной част и 150-300 г.
Кольцо-пробоотборник диаметром 80 мм, высотой 60 мм по ГОСТ 5182-78.
Нож.
Набор грузов.
Вазелин технический.
3. Подготовка к испытанию
3.1. Из монолита грунта вырезают образец кольцом-пробоотборником по ГОСТ 5182 – 78.
3.2. Отбирают пробу на влажность по ГОСТ 5180- 78.
Конус пенетрометра смазывают тонким слоем вазелина.
4. Проведение испытания
4.1. Кольцо с образцом помещают на столик пенетрометра, подводят острие конуса к поверхности грунта, закрепляют подвижную часть пенетрометра, индикатор устанавливают на нулевую отметку.
4.2. Убрав защелку
пенетрометра, позволяют конусу свободно внедряться в образец в течение 30 -60
с, отмечая его погружение по индикатору.
4.3. Дальнейшее вдавливание конуса про и сход и т путем приложения возрастающей ступеням и нагрузки. Ступени нагрузки на конус выбирают в зависимости от консистенции испытываемого грунта :
текучая – 0,05 кг;
текучепластичная – 0, 1 5 кг;
мягкопластичная – 0,3 кг;
тугопластичная – 0.5 кг;
полутвердая -0,75 кг;
твердая – 1 кг.
4.4. Каждую ступень нагрузки выдерживают до условной стабилизации реформации, составляющей не более 0, 1 мм за 30 с.
4.5. При каждом испытании осуществляют 6-9 ступеней нагрузки. Общая глубина погружения конуса должна достигать 15-20 мм.
4.6. Результаты опытов записывают в журнал.
5. Обработка результатов испытаний
5.1. По данным
каждого опыта строят график зависимости квадрата глубины погружения конуса h2
от вертикального усилия, передаваемого на конус Р, на котором точки
должны располагаться на прямой, выходящей из начала координат (см.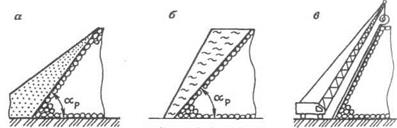 рисунок).
рисунок).
В этом случае для определения Рп с графика снимают любое значение Р и соответствующее ему значение h2 .
5.2. В случае отклонения точек от одной прямой Рп определяют как среднее из полученных его значений на каждой ступени нагрузки.
5.3. В случае, когда график зависимости h2 от Р, пересекает ось Р, от значения Р вычитают поправку Рх
5.4. За нормативное значение Рп принимают среднее значение опытов по верхней и нижней поверхностям образца.
5.5. Наименование пылевато-глинистых грунтов по удельному сопротивлению пенетрации приведены в табл. 1.
1 – Рп определяется по любой точке; 2 – Рп определяется по среднему арифметическому из частных значений; 3 – из значений Р вычитается Рх
Таблица 1
Наименование пылевато-глинистых грунтов по удельному сопротивлению пенетрации
|
Наименование грунтов |
Удельное сопротивление пенетрации Рп , кг/см 2 |
|
Очень прочные |
> 2 |
|
Прочные |
2 – 1 |
|
Средней прочности |
1 – 0,5 |
|
Слабые |
< 0,5 |
Журнал испытания пылевато-глинистых грунтов на удельное сопротивление пенетрации
|
№ п/п |
Дата |
Номера пробы |
Номер выработки |
Глубина отбора пробы, м |
Нагрузка на конус Р, кг |
Глубина погружения конуса h , см |
h2 , см2 |
Поправка Рх |
Удельное сопротивление пенетрации Рп, кг/см2 |
Примечание |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Рекомендуемое
МЕТОД ОПРЕДЕЛЕНИЯ УГЛА ЕСТЕСТВЕННОГО ОТКОСА
Настоящая
методика распространяется на песчаные грунты и устанавливает метод
лабораторного определения угла естественного откоса.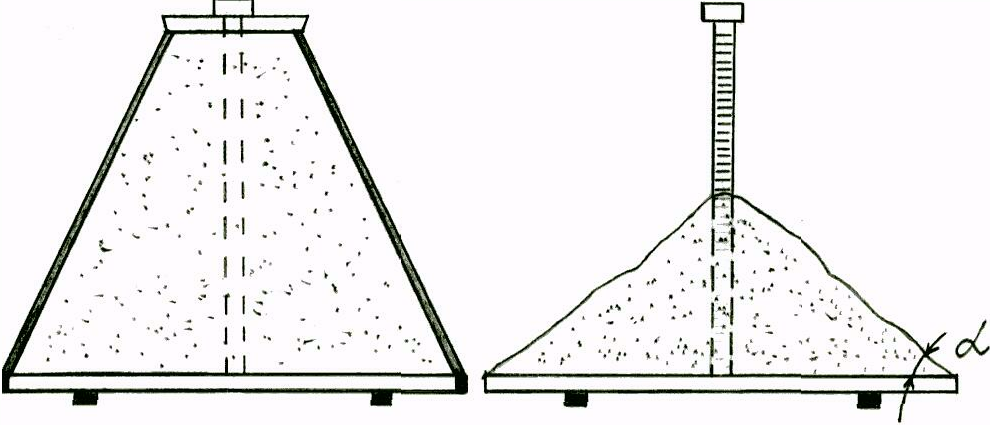
Методика не распространяется на песчаные грунты, содержащие более 3 % органических веществ.
1. Общие положения
1.1. Углом естественного откоса называется предельный угол наклона откоса, при котором грунт находится в устойчивом состоянии.
1.2. Угол естественного откоса песчаных грунтов определяют на воздухе и под водой.
1.3. Каждое определение выполняют с двукратной повторностью.
1.4. Точность определения угла естественного откоса – 1 °.
2. Аппаратура
Прибор УВТ-3.
Сито с сеткой № 2 по ГОСТ 3584-73.
Чашка фарфоровая по ГОСТ 9147 -73.
Противень лабораторный.
Воронка конусообразная с длинным стеблем № 7.
3. Подготовка к испытанию
3.1. Песчаный грунт высушивают на воздухе и просеивают через сито с сеткой № 2.
3.2. Отбирают
среднюю пробу грунта.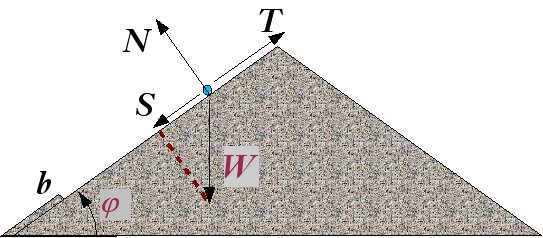
3.3. При проведении испытания на воздухе сухой прибор УВТ-3 устанавливают на противень (без ванны), при проведении испытания под водой – в ванну прибора УВТ-3.
4. Проведение испытания
4.1. Обойму заполняют песком через воронку до полного заполнения.
4.2. При проведении испытания под водой ванну заполняют водой до шейки обоймы. Насыщение песка водой продолжают до потемнения поверхности песка в обойме.
4.3. Осторожным движением вверх снимают обойму.
5. Обработка результатов
Отсчет в градусах берут по вершине стабилизировавшегося конуса, соприкасающийся с градуированной стойкой столика прибора УВТ-3.
Рекомендуемое
МЕТОД ОПРЕДЕЛЕНИЯ СЖИМАЕМОСТИ ЭЛЮВИАЛЬНЫХ ГРУНТОВ
Настоящая методика распространяется на элювиальные пылевато-глинистые
грунты твердой и полутвердой консистенции, а также песчаные грунты и
устанавливает способ лабораторного определения их сжимаемости в компрессионных
приборах.
Методика не распространяется на грунты, содержащие крупнообломочные включения более 20 %, а также обломки более 10 мм.
1. Общие положения
Соответствует ГОСТ 23908-79.
Для выяснения анизотропии сжимаемости, для образцов элювиальных грунтов компрессионные исследования проводят в двух взаимно перпендикулярных направлениях.
2. Аппаратура
Соответствует ГОСТ 23908-79.
Площадь одометров принимают в зависимости от размеров и содержания по массе обломочного материала:
при содержании обломков менее 5 мм – не менее 40 см 2
при содержании обломков 5 – 10 мм – не менее 100 см 2
3. Подготовка к испытаниям
Соответствует ГОСТ 23908-79.
4. Проведение испытания
4.1. Структурную прочность (Рстр) элювиальных грунтов определяют путем нагружения образцов ступенями давления по 0,0025 МПа до начала сжатия, характеризуемого относительной деформацией 0,005
4. 2. Начальную ступень давления принимают 0,05 МПа.
2. Начальную ступень давления принимают 0,05 МПа.
4.3. Дальнейшие ступени давления принимают 0,1 МПа.
4.4. После приложения каждой ступени давления регистрируют показания индикаторов через интервалы времени 0,25; 1; 10; 30; 60 мин, 2 ч до достижения условной стабилизации деформаций.
4.5. Условная стабилизация деформации не более 0,01 мм;
для пылевато-глинистых грунтов – за 12 ч;
для песчаных грунтов – за 6 ч.
Далее проведение испытаний соответствует ГОСТ 23908-79.
5. Обработка результатов испытаний
Соответствует ГОСТ 23908-79.
Значения поправки b за отсутствие поперечного расширения грунта в копрессионном приборе для:
песков пылеватых и мелких 0,75
песков средней крупности, крупных 0,85
супесей 0,7
суглинков твердых и полутвердых 0,6
глин твердых и полутвердых 0,8
Рекомендуемое
МЕТОД ОПРЕЛЕЛЕНИЯ КОЭФФИЦИЕНТА ВЫВЕТРЕЛОСТИ
Настоящая методика
распространяется на крупнообломочные элювиальные грунты и устанавливает метод
лабораторного определения коэффициента выветрелости.
1. Общие положения
1.1. Коэффициент выветрелости К следует определять по формуле:
(1)
где К1– отношение массы частиц размером менее 2 мм к массе частиц размером более 2 мм после испытания на истирание,
Ко – то жо до испытан и я на истирание.
1.2. Квк– определяют для крупнообломочного элювия магматических и метаморфических грунтов, содержащих не менее 10% по массе заполнителя частиц размером менее 2 мм.
Для крупнообломочного элювия осадочных грунтов содержание заполнителя не регламентируется.
1.3. Разделение образца грунта на фракции и определение массы частиц размером менее и более 2 мм проводят по ГОСТ 12536-79.
1.4. Взвешивания производят с точностью ± 1г
1. 5. Результаты
вычисления Квк должны иметь погрешность не более 0,01.
5. Результаты
вычисления Квк должны иметь погрешность не более 0,01.
2. Аппаратура
Полочный барабан со скоростью вращения 50-70 об/мин.
Сито с сеткой № 2 по ГОСТ 3584-73 с поддоном.
Весы лабораторные с пределом взвешивания 5 кг по ГОСТ 19491-74.
3. Подготовка к испытания м
3.1. Отбирают среднюю пробу массой 2-2,5 кг, избегая «круглых» значений 2 или 2,5 кг.
3.2. Проводят просеиванием грунта через сито № 2 разделение на мелкозем и обломки.
3.3. Устанавливают массу мелкозема т1 и обломков т2.
4. Проведение испытаний
4.1. Образец загружают в полочный барабан.
4.2. Испытания проводят циклами вращения барабана по 2 мин, устанавливая каждый раз просеиванием массу мелкозема и обломков .
4.3. Испытания проводят
до тех пор, пока выход мелкозема после очередного цикла по массе станет равным
1% или менее от начальной массы пробы. Установленные для этого момента значения
и используют для определения максимальной степени разрушения
обломков и расчета К1.
Установленные для этого момента значения
и используют для определения максимальной степени разрушения
обломков и расчета К1.
4.4.. К случае увеличения выхода мелкозема за первые 2 цикла менее 10% от обломки следует относить к прочным, грунт оценивать как невыветрелый и испытание прекратить.
4.5. В случае увеличения выхода мелкозема в пределах 10 – 25 % от за природную степень разрушения принимают отношение т 1 к т 2 после четырехминутного испытания в барабане.
4.6. В случае увеличения выхода мелкозема более 25% за К принимают значение, установленное до начала испытания.
4.7. Полученные значения масс мелкозема и обломков, соответствующие различным циклам, заносят в журнал.
5. Обработка результатов
5.1. К вычисляют по формуле ( 1).
5.2.
Наименование крупнообломочных грунтов по степени выветрелости в зависимости от Квкприведено в табл. 1.
1.
Таблица 1
Наименование крупнообломочных грунтов по степени выветрелости
|
Наименование грунтов |
Коэффициент выветрелости |
|
Невыветрелые |
0-0,5 |
|
Слабовыветрелые |
0,5-0,7 5 |
|
Сильновыветрелые |
0,75 -1 |
Угол естественного откоса – Энциклопедия по машиностроению XXL
Найти угол естественного откоса земляного грунта, если коэффициент трения для этого грунта f = 0,8.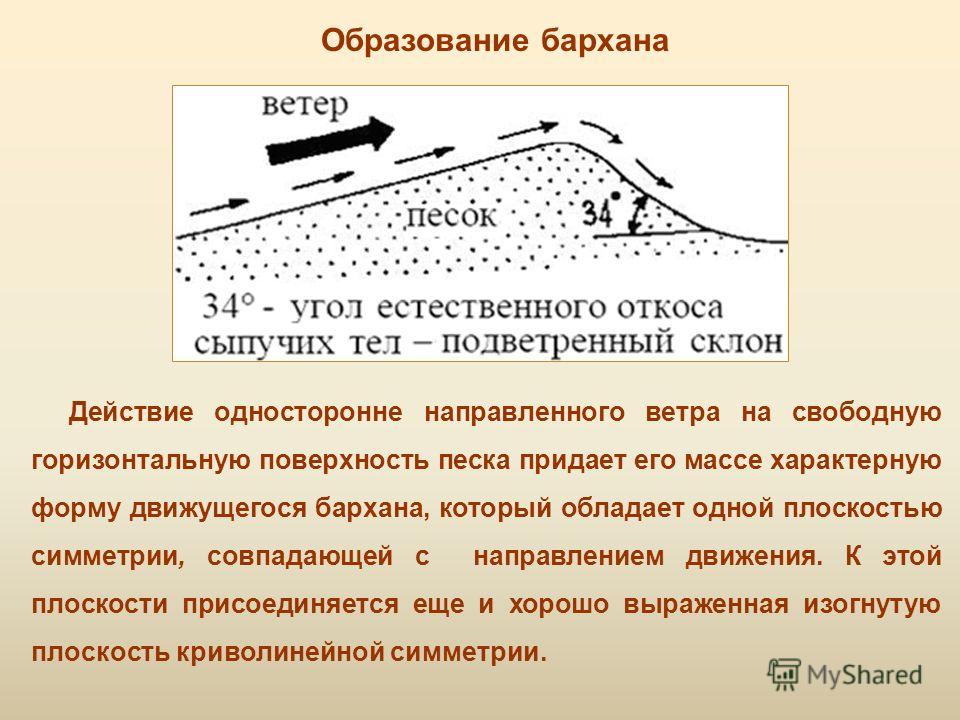 [c.53]
[c.53]Задача № 26. Идеально сыпучее тело, лежащее на горизонтальной плоскости, принимает форму конуса. Определить угол наклона образующей к горизонтальной плоскости угол естественного откоса). [c.95]
Но коэффициент трения, как известно, равен тангенсу угла треиия, следовательно, угол естественного откоса равен углу трения [c.95]
Угол естественного откоса, называемый также углом ската, имеет большое значение при проектировании различных насыпей, элеваторов, овощехранилищ и пр. [c.95]
Угол естественного откоса 95 [c.457]
Угол естественного откоса 169 [c.302]
Угол трения, конус трения и угол естественного откоса [c.248]
Определим угол естественного откоса и докажем, что он равен углу трения между частицами песка, лежащими на боковой поверхности сыпучего тела. Рассмотрим частицу песка М, лежащую на
[c.250]
Рассмотрим частицу песка М, лежащую на
[c.250]
Следовательно, угол естественного откоса равен углу трения. Это можно рассматривать как еще одну физическую интерпретацию угла трения. [c.250]
Угол естественного откоса 250 [c.455]
Сухой песок насыпан на горизонтальную площадку в кучу, имеющую форму конуса (рис, 125). Определить угол естественного откоса [c.156]
Наибольший угол, который составляет с горизонтом наклонная плоскость, образованная сыпучим телом, называется углом естественного откоса. Угол естественного откоса сыпучего тела равен углу трения между его частицами. Этот угол приходится принимать во внимание, например, при различных земляных работах. [c.54]
Геометрические схемы установки ленточных конвейеров разнообразны. Наиболее ходовые из них приведены в табл. 2. Простейшими и часто применяемыми являются схемы а и б с одним прямолинейным участком. Далее следуют схемы с двумя и тремя участками (в, г, д, е, ж, з). Угол наклона ленты к горизонту допускается обычно до 18—25° [(0,45—0,5)[c.1037]
Далее следуют схемы с двумя и тремя участками (в, г, д, е, ж, з). Угол наклона ленты к горизонту допускается обычно до 18—25° [(0,45—0,5)[c.1037]
Кривая поверхности сыпучего материала в ковшах элеватора закономерно связана с кривой поверхности жидкости, отклоняясь от неё на угол естественного откоса, вследствие чего поверхность сыпучего материала располагается в ковшах при обходе барабана не по окружности, а по логарифмической спирали с центром в точке Р. Без существенного ущерба для точности можно заменить логарифмическую спираль в зоне ковшей прямой линией, так как здесь радиусы кривизны спирали оказываются достаточно большими. [c.1087]
Грунт, выброшенный из котлована, следует размещать на расстоянии не менее 0,5 ju от бровки. Для вь. емок с откосами, крутизна которых превышает угол естественного откоса данного грунта, предельное расстояние выброшенного грунта от бровок надлежит заранее уточнять расчетом. До начала разработки выемок должны быть осуществлены мероприятия по отводу поверхностных вод от мест расположения выемок. [c.1022]
[c.1022]
Угол естественного откоса при насыпа-нии, г рад [c.44]
Насыпной вес и угол естественного откоса для различных топлив составляют (см. табл. вверху в правой колонке). [c.427]
Если не учитывать влияние частиц продукта друг на друга, их отдаленности от оси барабана и угол естественного откоса, то пропускную способность гладкого барабана можно определить по выражению [c.51]
Сушилка распылительная с центробежно-дисковым распылом с нихсушильного агента и коническим днищем 1500—25 ООО Малая вязкость, малый угол естественного откоса сухого продукта, большая продолжительность сушки [c.189]
Сушилка распылительная с центробежно-дисковым распылом с верхним подводом сушильного агента и плоским днищем 500—20 ООО Малая вязкость, большой угол естественного откоса сухого продукта, большая длительность второго периода сушки
[c. 189]
189]
Здесь Q и V — заданная производительность конвейера соответственно в т час й M jna 7—насыпной вес материала в V — скорость ленты в м/сек (рекомендуемые скорости приведены в табл. 6 при применении разгрузчиков предельные значения скорости должны быть увязаны со значениями по табл. 5) зерна —35°) С — коэфициент насыпки в зависимости от угла наклона конвейера приведён в табл. 7. [c.1043]
В среднем, для ненапряжённых условий работы конвейера, можно принимать ft = 0.85 и р = 0,5р, где р — угол естественного откоса материала в условиях движения. При форсированной работе конвейера (если некоторая просыпь перемещаемого материала не является существенной) эти величины можно повышать до следующих значений к = 0,97 и р” = 0,75р. Величины коэфициента с при гладкой ленте могут быть приняты следующие [c.1125]
Видимое отсутствие застойных зон могло быть следствием работы с очень большими скоростями фильтрации По крайней мере проведенная авторами (Л. 535] киносъемка движения частиц над горизонтальной пластинкой шириной всего 50 мм, размещаемой в псевдо-ожиженном слое на разных уровнях, в том числе в плоскости решетки, показала наличие застойных зон. Авторы [Л. 535] закрепляли пластинку на высоте О—200 мм от решетки в двухмерном (9—380 мм) псевдоожижен-ном слое катализатора крекинга нефти (частицы 75— 100 мкм г0п.у=О,б2 см1сек угол естественного откоса 29,4°). Над пластинкой возникала мертвая зона неподвижного материала. Выше мертвой зоны находилась квазистабильная застойная зона , материал (В которой периодически (1 раз в несколько секунд) сменялся за счет пульсаций окружаюш,его слоя. Зависимость высоты мертвой зоны от типа решетки (перфорированной с отверстиями 0 1 мм или пористой — из фильтровальной бумаги) и высоты расположения пластинки была незначительной. Она уменьшалась с увеличением скорости фильтрации до Л/ — 4, после чего оставалась почти неизменной. Впрочем, данных для N, больших 5,35, не указано, а при Л = 5,35 —мала форсировка для слоя столь мелких частиц.
535] киносъемка движения частиц над горизонтальной пластинкой шириной всего 50 мм, размещаемой в псевдо-ожиженном слое на разных уровнях, в том числе в плоскости решетки, показала наличие застойных зон. Авторы [Л. 535] закрепляли пластинку на высоте О—200 мм от решетки в двухмерном (9—380 мм) псевдоожижен-ном слое катализатора крекинга нефти (частицы 75— 100 мкм г0п.у=О,б2 см1сек угол естественного откоса 29,4°). Над пластинкой возникала мертвая зона неподвижного материала. Выше мертвой зоны находилась квазистабильная застойная зона , материал (В которой периодически (1 раз в несколько секунд) сменялся за счет пульсаций окружаюш,его слоя. Зависимость высоты мертвой зоны от типа решетки (перфорированной с отверстиями 0 1 мм или пористой — из фильтровальной бумаги) и высоты расположения пластинки была незначительной. Она уменьшалась с увеличением скорости фильтрации до Л/ — 4, после чего оставалась почти неизменной. Впрочем, данных для N, больших 5,35, не указано, а при Л = 5,35 —мала форсировка для слоя столь мелких частиц. [c.75]
[c.75]
Соблюдение этого условия, по-видимому, обеспечит и растекание материала по мелкой решетке, если только угол естественного откоса меньше 90°. В выражение П-52) для подсчета минимального ДРреш следует, конечно, подставлять не любое Я, а некоторое Ямин, при котором еще наблюдаются условия стесненного обтекания частиц, из-за чего действительно Wn.y воздушно-сухого фрезерного торфа. Тогда требуемое рабочее сопротивление мелкой решетки составит [c.79]
УГОЛ естественною откоса — угол трения для случая сьшучей среды зрения — угол, под которым в центре глаза сходятся лучи от крайних точек предмета или его изображения краевой — угол между поверхностью тела и касательной плоскостью к искривленной поверхности жидкости в точке ее контакта с телом Маха — угол между образующей конуса Маха и его осью падения (отражения или преломления)— угол между направлением распространения падающей (отраженной или преломленной) волны и перпендикуляром к поверхности раздела двух сред, на (от) которую (ой) падает (отражается) или преломляется волна предельный полного внутреннего отражения — угол падения, при котором угол преломления становится равным 90 прецессии — угол Эйлера между осью А неподвижной системы координат и осью нутации, являющейся линией пересечения плоскостей xOj и x Of (неподвижной и подвижной) систем координат сдвига—мера деформации скольжения — угол между нада ющнм рентгеновским лучом и сетчатой плоскостью кристалла телесный — часть пространства, ограниченная замкнутой кони ческой поверхностью, а мерой его служит отношение нлоща ди, вырезаемой конической поверхностью на сфере произволь ного радиуса с центром в вершине конической поверхности к квадрату радиуса этой сферы трения—угол, ташенс которого равен коэффициенту трения скольжения) УДАР [—совокупность явлений, возникающих при столкновении движущихся твердых тел с резким изменением их скоростей движения, а также при некоторых видах взаимодействия твердого тела с жидкостью или газом абсолютно центральный неупругий прямой возникает, если после удара тела движутся как одно целое, т. е. с одной и той же скоростью упругий косой и прямой возникают, если после удара тела движутся с неизменной суммарной кинетической энергией) ]
[c.288]
е. с одной и той же скоростью упругий косой и прямой возникают, если после удара тела движутся с неизменной суммарной кинетической энергией) ]
[c.288]
Сушилка распылительная с форсуночным распылом, верхним подводом сушильного агента и конусным днищем 5-3000 Большая начальная вязкость, но жндкотекучесть, наличие абразивных включений, малый угол естественного откоса сухого продукта, малая длительность процесса сушки [c.189]
Естественный откос щебня. Определение угла естественного откоса песчаного грунта
Углом естественного откоса φ, град., называется угол, при котором неукрепленный откос песчаного грунта сохраняет равновесие или угол наклона поверхности свободно насыпанного грунта к горизонтальной плоскости.
Определение угла естественного откоса имеет важное значение при проектировании грунтовых сооружений: насыпных и намывных плотин, дорожных насыпей, дамб обвалования, хвостохранилищ, а также для оценки устойчивости естественных откосов и для проведения мероприятий но их укреплению.
В тех случаях, когда сопротивление сдвигу” частиц определяется лишь силами трения. угол естественного откоса совпадает с углом внутреннего трения {φ = φо ). Однако в реальных грунтах сопротивление сдвигу” зависит не только от сил трения, но также от зацепления частиц и других факторов, влияющих на φ, т. е.
где φ р, – составляющая за счет трения; φ Л – то же, за счет зацепления; φ с – то же, за счет среза частиц.
Составляющая φ Т зависит от минерального состава частиц, наличия поверхностных пленок и др., φ Л – от шероховатости поверхности и плотности упаковки частиц, а φ с – от окатанности и формы частиц грунта. Поэтому значения φ и φ о обычно различаются, особенно для плотных и неоднородных по структуре песков. Однако угол естественного от
коса φ о является легко определяемой и удобной характеристикой прочности несвязных грунтов. Способ применяется только для приближенного определения величины внутреннего трения сыпучих грунтов – чистых песков.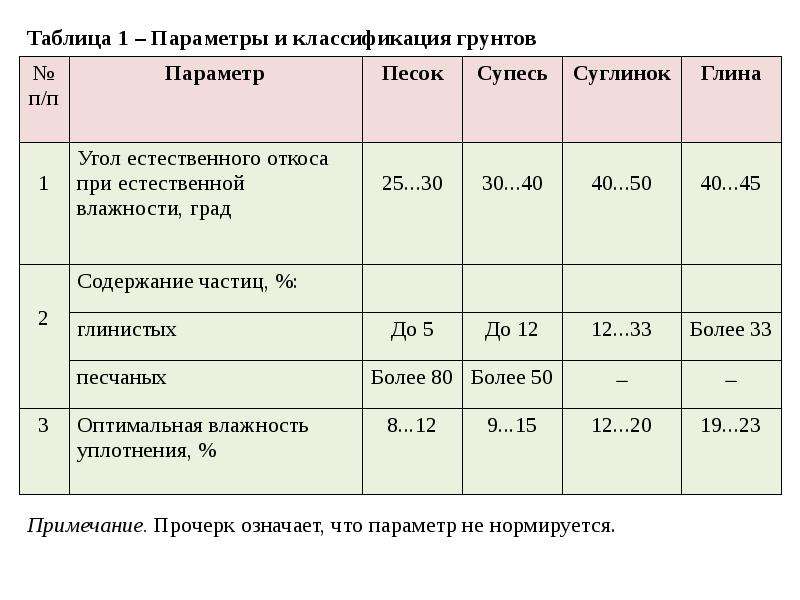 В чистых песках приближенно величина угла внутреннего трения соответствует углу естественного откоса, т. с. углу, при котором неукрепленный откос песчаного грунта является устойчивым .
В чистых песках приближенно величина угла внутреннего трения соответствует углу естественного откоса, т. с. углу, при котором неукрепленный откос песчаного грунта является устойчивым .
Угол естественного откоса определяют на приборе УВТ (рис. 8.44), который состоит из металлического столика-поддона, обоймы и резервуара. Поддон установлен на тpex опорах и перфорирован отверстиями диаметром 0,8…1,0 мм для водонасыщения песка. Шкала, укрепленная в центре столика-поддона, имеет деления от 5° до 45°, по которым определяется угол откоса.
Рис. 8.44. Прибор для определения угла естественного откоса песчаных грунтов: а схема прибора: 1 резервуар: 2 крышка резервуара: 3 обойма: 4 столик: 5 перфорированное дно: 6 – шкала: 7 – опора: б – общий вид приборов
Определение угла естественного откоса в воздушно-сухом состоянии . На столик устанавливают обойму, в которую через воронку насыпают песок до ее заполнения, слегка постукивая по обойме.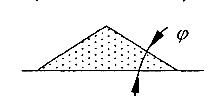 Осторожно, стараясь не рассыпать песок, вертикально поднимают обойму и но вершине образовавшегося песчаною конуса берут отсчет по шкале.
Осторожно, стараясь не рассыпать песок, вертикально поднимают обойму и но вершине образовавшегося песчаною конуса берут отсчет по шкале.
Опыт повторяют 3 раза и рассчитывают среднее арифметическое показание. Расхождение между повторными определениями не должно превышать 1 градус.
Определение угла естественного откоса песка под водой . После заполнения обоймы песком резервуар наполняют водой и после полного насыщения пробы определяют угол естественного откоса.
Для предварительного назначения откосов котлованов и карьеров рекомендуется руководствоваться значениями углов, близкими к углам естественного откоса грунта (табл. 8.61).
Таблица 8.61
Угол естественного откоса насыпных грунтов
На величину угла естественного откоса (#>”) несвязных грунтов влияет однородность их гранулометрического состава: монодисперсные грунты обладают большим значением φо, чем полидисперсные грунты такого же минерального состава. Это объясняется тем, что в смеси мелкие частицы заполняют промежутки между крупными, что облегчает их смешение по поверхности откоса.
Это объясняется тем, что в смеси мелкие частицы заполняют промежутки между крупными, что облегчает их смешение по поверхности откоса.
Большое влияние на трение между частицами несвязного грунта оказывает наличие в грунте жидкостей, присутствие которых снижает φ. В несвязных песчаных грунтах влажность существенно влияет на угол внутреннего трения. С ростом влажности песка до максимальной молекулярной влагоемкости величина φо закономерно снижается за счет постепенного уменьшения трения и достигает минимума при максимальной молекулярной влагоемкости. Дальнейшее увеличение влажности песка приводит к образованию капиллярной связности между частицами; за счет этого угол внутреннего трения начинает увеличиваться и достигает максимума при влажности капиллярной влагоемкости, когда силы капиллярного притяжения между частицами наибольшие. Последующее увеличение влажности песка снижает капиллярную связность, трение на контактах частиц снижается, и угол внутреннего трения постепенно уменьшается, достигая минимального значения в состоянии полного водонасыщения песка .
Общие положения
Назначение и виды земляных сооружений
Объем земляных работ очень большой, он имеется при строительстве любого здания и сооружения. Из общей трудоемкости в строительстве земляные работы составляют 10%.
Различаются следующие основные виды земляных сооружений :
Планировка площадки;
Котлованы и траншеи;
Земляные полотна дорог;
Плотины;
Каналы и др.
Земляные сооружения делятся на :
Постоянные;
Временные.
К постоянным относятся котлованы, траншеи, насыпи, выемки.
К постоянным земляным сооружениям предъявляются требования :
Должно быть прочным, т.е. сопротивляться временным и постоянным нагрузкам;
Устойчивым;
Хорошо сопротивляться атмосферным влияниям;
Хорошо сопротивляться размывающим действиям;
Должны обладать безосадочностью.
Основные строительные свойства и классификация грунтов
Грунтом называют породы, залегающие в верхних слоях земной коры. К ним относятся: растительный грунт, песок, супесь, гравий, глина, суглинок лессовидный, торф, различные скальные грунты и плывуны.
К ним относятся: растительный грунт, песок, супесь, гравий, глина, суглинок лессовидный, торф, различные скальные грунты и плывуны.
По крупности минеральных частиц и их взаимной связи различают следующие грунты :
Связные – глинистые;
Несвязные – песчаные и сыпучие (в сухом состоянии), крупнообломочные несцементированные грунты содержащие более 50% (по массе) обломков кристаллических пород размером более 2 мм;
Скальные – изверженные, метаморфические и осадочные породы с жесткой связью между зернами.
К основным свойствам грунтов, влияющим на технологию производства, трудоемкость и стоимость земляных работ относятся :
Объемная масса;
Влажность;
Размываемость
Сцепление;
Разрыхленность;
Угол естественного откоса;
Объемной массой называется масса 1 м3 грунта в естественном состоянии в плотном теле.
Объемная масса песчаных и глинистых грунтов 1,5 – 2 т/м3, скальных не разрыхленных до 3 т/м3.
Влажность – степень насыщения пор грунта водой
g b – g c – масса грунта до и после сушки.
При влажности до 5% – грунты называются сухие. При влажности от 5 до 15% – грунты называются маловлажными. При влажности от 15 до 30% – грунты называются влажные.
При влажности более 30% – грунты называются мокрые.
Сцепление – начальное сопротивление грунта сдвигу.
Сила сцепления грунтов : – песчаных грунтов 0,03 – 0,05 МП- глинистых грунтов 0,05 – 0,3 МП- полускальных грунтов 0,3 – 4 МПа- скальных более 4 МПа.
В мерзлых грунтах сила сцепления значительно больше.
Разрыхляемость – это способность грунта увеличиваться в объеме при разработке, вследствие потери связи между частицами. Увеличение объема грунта характеризуется коэффициентом разрыхления К р. После уплотнения разрыхленного грунта называется остаточной разрыхленностью К ор.
Угол естественного откоса характеризуется физическими свойствами грунта. Величина угла естественного откоса зависит от угла внутреннего трения, силы сцепления и давления вышележащих слоев. При отсутствии сил сцепления предельный угол естественного откоса равен углу внутреннего трения. Крутизна откоса зависит от угла естественного откоса. Крутизна откосов выемок и насыпей характеризуется отношением высоты к заложению m – коэффициент откоса.
Величина угла естественного откоса зависит от угла внутреннего трения, силы сцепления и давления вышележащих слоев. При отсутствии сил сцепления предельный угол естественного откоса равен углу внутреннего трения. Крутизна откоса зависит от угла естественного откоса. Крутизна откосов выемок и насыпей характеризуется отношением высоты к заложению m – коэффициент откоса.
Углы естественного откоса грунтов и отношение высоты откоса к заложению
| Грунты | Значение углов естественного откоса и отношений высоты откоса к его заложению при различной влажности грунтов | |||||
| Сухой | Влажный | Мокрый | ||||
| Угол в град | Угол в град | Отношение высоты к заложению | Угол в град | Отношение высоты к заложению | ||
| Глина | 1: 1 | 1: 1,5 | 1: 3,75 | |||
| Суглинок средний | 1: 0,75 | 1: 1,25 | 1: 1,75 | |||
| Суглинок легкий | 1: 1,25 | 1: 1,75 | 1: 2,75 | |||
| Песок мелкозернистый | 1: 2,25 | 1: 1,75 | 1: 2,75 | |||
| Песок среднезернистый | 1: 2 | 1: 1,5 | 1: 2,25 | |||
| Песок крупнозернистый | 1: 1,75 | 1: 1,6 | 1: 2 | |||
| Растительный грунт | 1: 1,25 | 1: 1,5 | 1: 2,25 | |||
| Насыпной грунт | 1: 1,5 | 1: 1 | 1: 2 | |||
| Гравий | 1: 1,25 | 1: 1,25 | 1: 1,5 | |||
| Галька | 1: 1,5 | 1: 1 | 1: 2,25 |
Размываемость грунта – унос частиц текучей водой.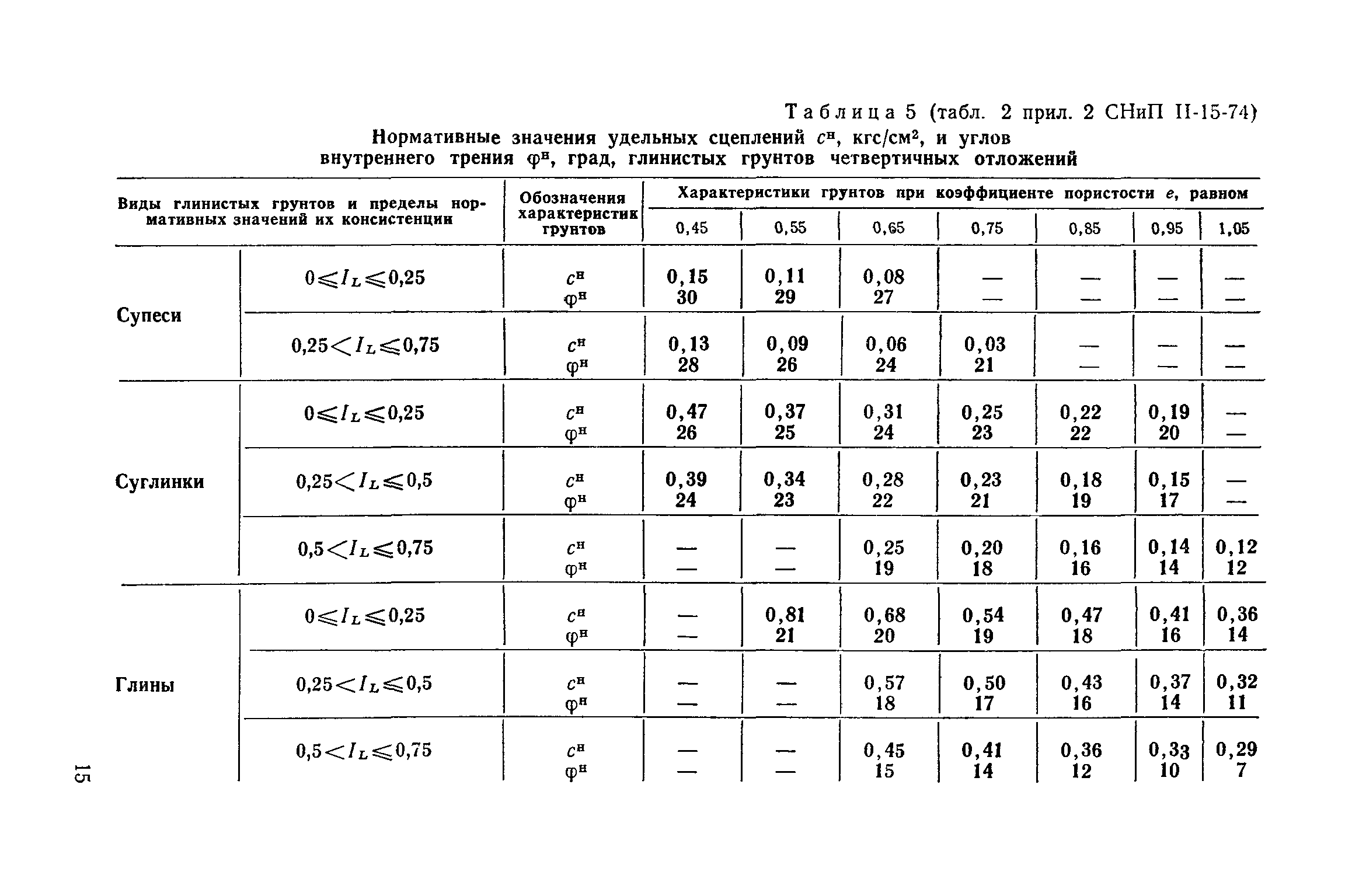 Для мелких песков наибольшая скорость воды не должна превышать 0,5-0,6 м/сек, для крупных песков 1-2 м/сек, для глинистых грунтов 1,5 м/сек.
Для мелких песков наибольшая скорость воды не должна превышать 0,5-0,6 м/сек, для крупных песков 1-2 м/сек, для глинистых грунтов 1,5 м/сек.
Цель работы:
Ознакомление с методикой определения угла естественного откоса для песчаных грунтов.
Приобретение навыков в работе с прибором для определения угла естественного откоса сыпучих грунтов.
Определение угла естественного откоса песка в воздушно-сухом и подводном состоянии.
Необходимое оборудование и материалы
Методические указания к выполнению работы.
Журнал лабораторных работ.
Прибор для определения угла естественного откоса полевой лаборатории Литвинова.
Емкость с водой.
Отсутствие сцепления в песках позволяет определять угол внутреннего трения φ 0 по углу естественного откоса грунта в условиях предельного равновесия (рис. 2.3.).
Рис.2.3. Схема к определению угла естественного откоса песчаного гранта.
T 1 =
где φ – угол внутреннего трения; tg φ – коэффициент трения
Углом
естественного откоса песчаного грунта
называют максимальное значение угла,
образуемого с горизонтальной плоскостью,
поверхностью грунта, отсыпанного без
толчков и динамических воздействий.
Угол естественного откоса определяют для песчаного грунта в воздушно-сухом состоянии и под водой. Для испытания используем прибор Литвинова.
Порядок выполнения работы
Определение угла естественного откоса грунта в воздушно-сухом состоянии производят следующим образом. Прибор устанавливают на стол, выдвижная створка при этом опущена до дна. В малое отделение прибора до верха засыпают испытываемый песок (рис.2.4). После этого постепенно поднимают выдвижную створку без толчков; при этом прибор придерживают рукой. Грунт постепенно частично пересыпается в другое отделение до наступления положение равновесия.
Рис. 2.4. Общий вид прибора для определения угла естественного откоса песков (Ящик Кулона).
Угол
между плоскостью свободного откоса и
горизонтальной плоскостью и есть угол
естественного откоса. По делениям на
днище и боковой стенке отсчитывают
высоту и заложение откоса и вычисляют
тангенс угла естественного откоса;
отсчеты ведут с точностью до 1мм.
Определение угла естественного откоса грунта в подводном состоянии отличается от предыдущего тем, что после того, как в малое отделение прибора насыпают испытываемый грунт, в большое отделения до верха наливают воду. Верхнюю створку подымают на несколько миллиметров, чтобы вода могла проникнуть в малое отделение. Когда весь грунт пропитается водой, поднимают створку выше и испытание продолжают так же, как и предыдущее. Результаты испытаний заносят в таблицу 2.4.
Углом естественного откоса грунта называется наибольшее значение угла, который образует с горизонтальной плоскостью поверхность грунта, отсыпанного без толчков; сотрясений и колебаний.
Угол естественного откоса зависит от сопротивления грунта сдвигу. Для установления этой зависимости представим себе грунтовое тело, рассеченное плоскостью а – а, наклоненной к горизонту под углом а (рис. 22).
Часть грунта выше плоскости а – а, рассматриваемая как единый массив, может оставаться в покое или прийти в движение под действием силы P – собственного веса и воздействия возведенного на нем сооружения.
Разложим P на две силы: N = P cos а, направленную нормально к плоскости а – а и силу T = P sin а, параллельную плоскости а – а. Сила T стремится сдвинуть отсеченную часть, которая удерживается силами сцепления и трения в плоскости а – а.
В состоянии предельного равновесия, когда сдвигающая сила уравновешивается сопротивлением трения и сцепления, но когда сдвига еще нет, выполняется равенство 26, т. е. T = N tg ф + CF.
В глинистых грунтах сдвигу в основном противодействует сцепление.
В сухом песке сцепления почти нет и состояние предельного равновесия характеризуется соотношением T = N tg ф. Подставляя значения N и T, получим P sin а = P cos a tg ф или tg a = tg ф и а = ф, т. е. угол а соответствует углу внутреннего трения грунта ф в состоянии предельного равновесия массива несвязного грунта.
Определение угла естественного откоса песка показано на рис. 23. Угол естественного откоса песка определяют дважды – для состояния естественной влажности и под водой.
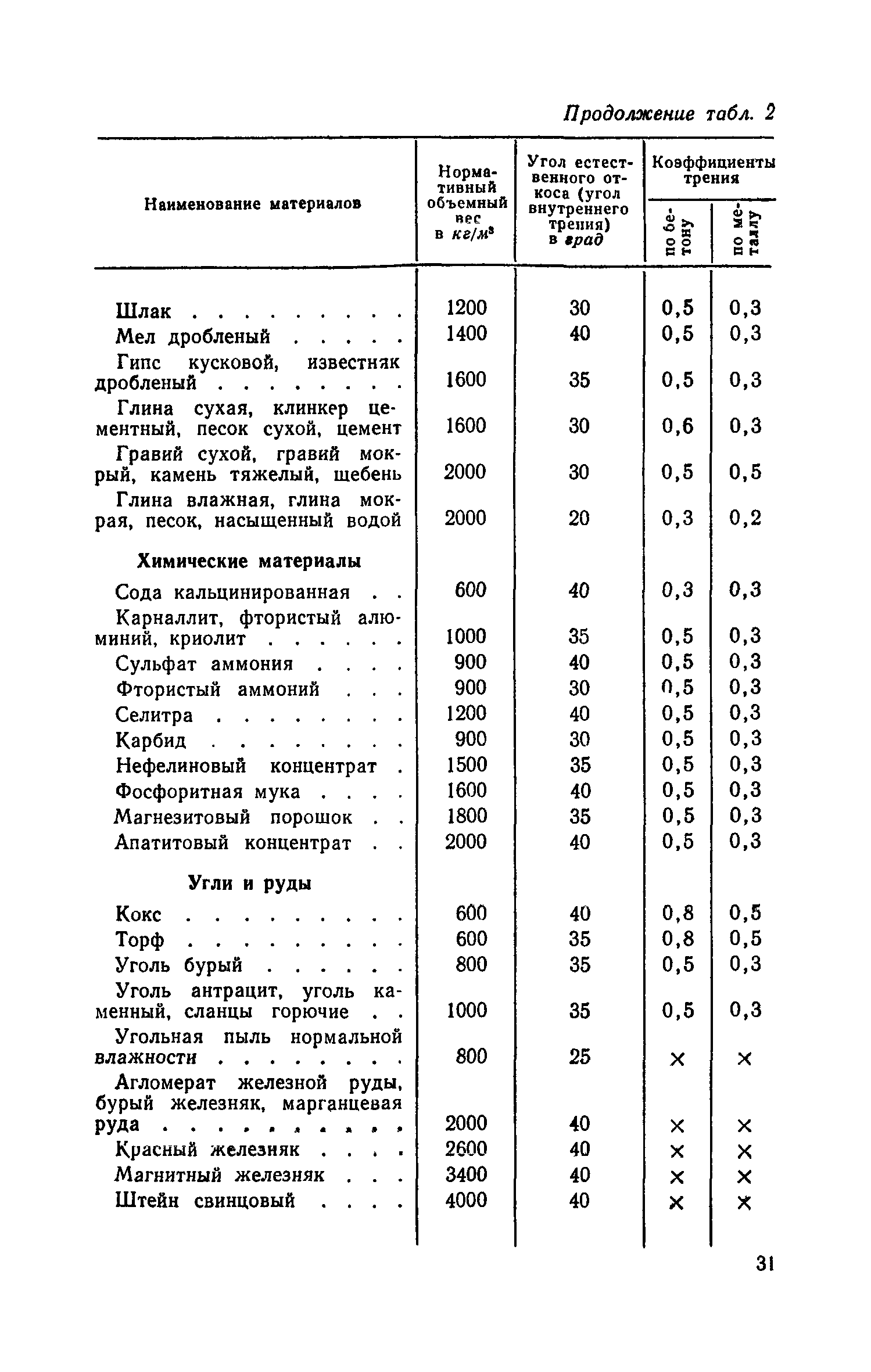 Для этого в стеклянный прямоугольный сосуд насыпают песчаный грунт, как показано на рис. 23, а. Затем сосуд наклоняют под углом не менее 45° и осторожно возвращают в прежнее положение (рис. 23, б). Далее определяется угол а между образовавшимся откосом песчаного грунта и горизонталью; о величине угла а можно судить по отношению hl, равному tg а.
Для этого в стеклянный прямоугольный сосуд насыпают песчаный грунт, как показано на рис. 23, а. Затем сосуд наклоняют под углом не менее 45° и осторожно возвращают в прежнее положение (рис. 23, б). Далее определяется угол а между образовавшимся откосом песчаного грунта и горизонталью; о величине угла а можно судить по отношению hl, равному tg а.В последние годы для определения характеристик сопротивления грунтов сдвигу предложен ряд новых методов: по данным испытания грунтов в стабилометрах (см. рис. 11), по вдавливанию шарикового штампа в грунт (рис. 24), аналогично определению твердости по Бринеллю и др.
Испытание грунта методом шариковой пробы (рис. 24) заключается в измерении осадки шарика S при действии на него постоянной нагрузки р.
Значение эквивалентного сцепления грунта определяется по следующей формуле:
где P – полная нагрузка на
D – диаметр шарика, см;
S – осадка шарика, см.
Величина сцепления сш учитывает не только силы сцепления грунта, но и внутреннее трение.
Для определения удельного сцепления с значение сш умножается на коэффициент К, который зависит от угла внутреннего трения ф (град).
В последние годы метод шариковой пробы стали применять в полевых условиях. В этом случае применяются полусферические штампы размером до 1 м (рис. 25).
Характеристики сдвига ф и с называются прочностными и точность их определения имеет большое значение при расчете оснований сооружений по прочности и устойчивости.
Лабораторная работа 1. Определение величины угла ссыпания и угла естественного откоса зернисто-кускового материала
Цель работы. Определить величины угла естественного откоса и угла ссыпания зернисто-кускового материала.
Теоретические положения . Зернисто-кусковой материал, лежащий на наклонной плоскости (например, на наклонной плоскости бункера , на наклонном ленточном транспортере и т. д.), при определенном угле наклона этой плоскости к горизонту начинает ссыпаться по ней. Такой предельный угол наклона называется углом ссыпания.
В зависимости от формы кусочков можно наблюдать два вида движения кускового материала по плоскости ссыпания: скольжение и перекатывание. Скольжение наблюдается при кусках с развитыми плоскими гранями; передвижению кусков здесь препятствует трение скольжения между гранями кусков и плоскостью ссыпания. Качение наблюдается при форме кусков, близкой к шару. В этом случае передвижение куска происходит как скатывание его, с сопротивлением трения качения.
Предельное состояние покоя слоя кускового материала на наклонной плоскости имеет место тогда, когда сила трения F равна проекции М силы тяжести G на эту плоскость (рисунок 1). С другой стороны, эта же сила трения пропорциональна нормальному давлению кускового материала на наклонную плоскость
F = M = fN ,
откуда f = М / N = tgα
где f – коэффициент трения, определяемый свойствами самого материала, равный tga ;
α –
угол ссыпания зернисто-кускового материала.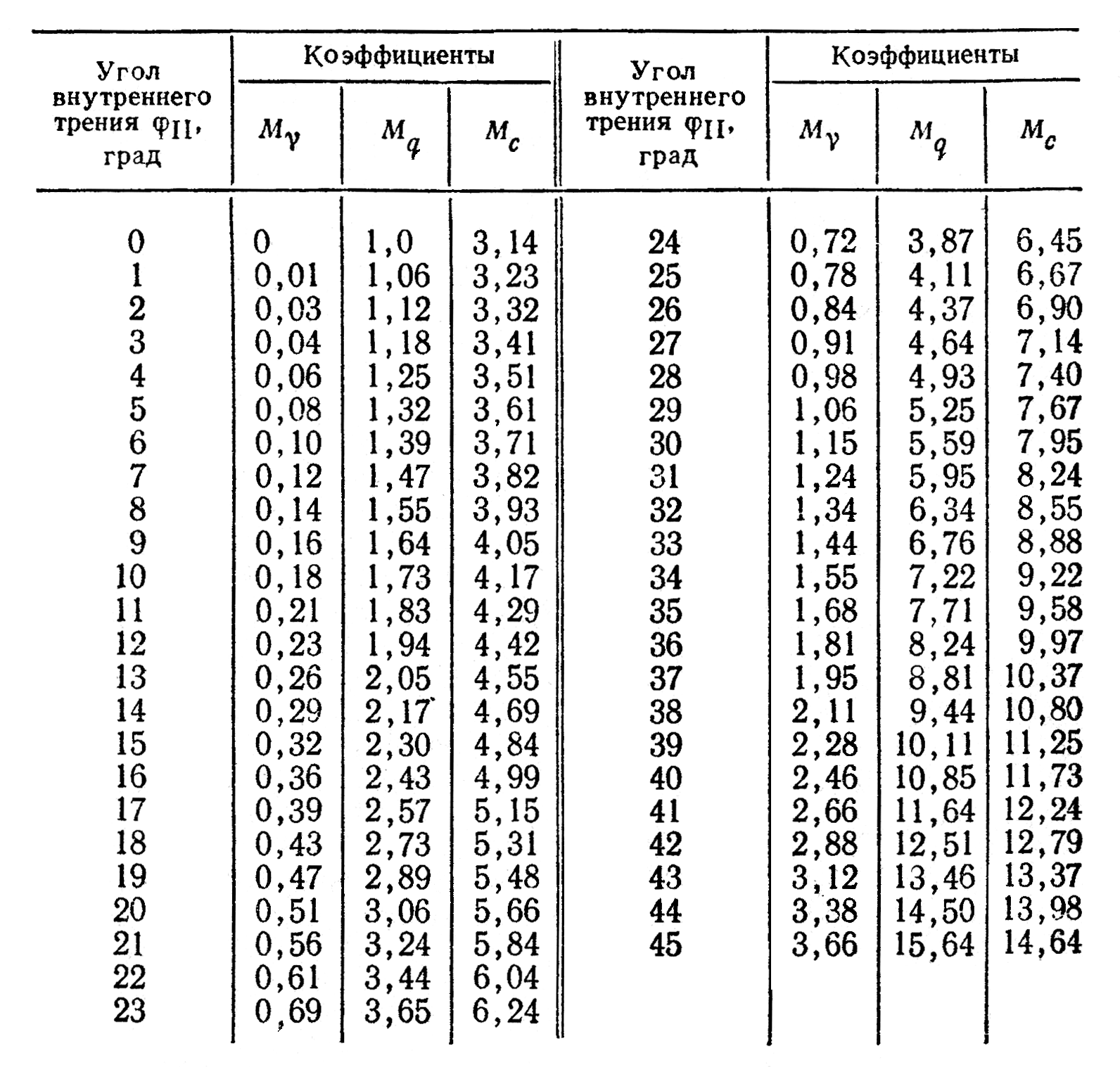
Рисунок 1
Если рассматривать весь слой сыпучего материала , который перемещается по гладкой наклонной плоскости, то здесь, даже в случае кусков шарообразной формы, происходит скорее скольжение материала по плоскости, чем перекатывание, так как весь материал «течет» сплошной массой.
Угол ссыпания зависит от коэффициента трения материала о плоскость ссыпания, от формы и крупности кусков, от структуры поверхности, по которой происходит ссыпание (поверхность может быть гладкой, шероховатой, ребристой и т. д.), а также он влажности самого кускового материала.
Если насыпать зернисто-кусковой материал на горизонтальную плоскость, то он располагается на ней в виде конуса. Угол между образующей этого конуса и горизонтальной плоскостью называется углом естественного откоса зернисто-кускового материала.
Угол естественного откоса всегда больше угла ссыпания (для одного и того же материала), так как наличие неровностей на поверхности материала препятствует скатыванию, а тем более скольжению кусков. Угол естественного откоса в большой степени зависит от фракционного состава кускового материала, ибо последний определяет собой общую структуру поверхности конуса. Эта разнородность размера кусков вызывает в то же время преимущественное скатывание крупных кусков материала на край насыпаемой кучи, вследствие того, что неровности поверхности оказывают меньшее сопротивление перекатыванию крупн
ых кусков, чем мелких (рисунок 2). Неравномерное распределение кусков по крупности необходимо учитывать при загрузке насадочных абсорберов, шахтных печей и т. д., так как в местах расположения крупных кусков, т. е. на-периферии, получается большее сечение каналов и газ пойдет преимущественно по этим каналам, имеющим меньшее гидравлическое сопротивление.
Угол естественного откоса в большой степени зависит от фракционного состава кускового материала, ибо последний определяет собой общую структуру поверхности конуса. Эта разнородность размера кусков вызывает в то же время преимущественное скатывание крупных кусков материала на край насыпаемой кучи, вследствие того, что неровности поверхности оказывают меньшее сопротивление перекатыванию крупн
ых кусков, чем мелких (рисунок 2). Неравномерное распределение кусков по крупности необходимо учитывать при загрузке насадочных абсорберов, шахтных печей и т. д., так как в местах расположения крупных кусков, т. е. на-периферии, получается большее сечение каналов и газ пойдет преимущественно по этим каналам, имеющим меньшее гидравлическое сопротивление.
Тонко измельченные материалы имеют больший угол естественного откоса, т. е. меньшую сыпучесть, в связи с более развитой поверхностью трения.
Рисунок 2
Угол естественного откоса значительно зависит от влажности материала, потому что вода, располагаясь на поверхности кусков, вызывает слипание их и тем самым затрудняет движение отдельных кусков. Чем меньше куски материала, тем больше проявляется влияние влажности; но чрезмерное увлажнение приводит к увеличению послойной текучести жидкости между кусочками материала, и угол естественного откоса вновь уменьшается (таблица 1).
Чем меньше куски материала, тем больше проявляется влияние влажности; но чрезмерное увлажнение приводит к увеличению послойной текучести жидкости между кусочками материала, и угол естественного откоса вновь уменьшается (таблица 1).
Таблица 1
Порода | Угол естественного откоса, град, для породы | ||
сухой | влажной | мокрой | |
Песок крупный | 30 – 35 | 32 – 40 | 25 – 27 |
Песок средний | 28 – 30 | ||
Песок мелкий | 30 – 35 | 15 – 20 | |
Гравий | 35 – 40 |
Угол естественного откоса и угол ссыпания резко уменьшаются при движении материала и плоскости, на которой он лежит. При сотрясениях или вибрациях материал интенсивно рассыпается, растекается, стремясь принять горизонтальное положение, так как при вибрациях в отдельные моменты уменьшается взаимное трение по поверхности соприкосновения кусочков друг с другом и кусочков с плоскостью.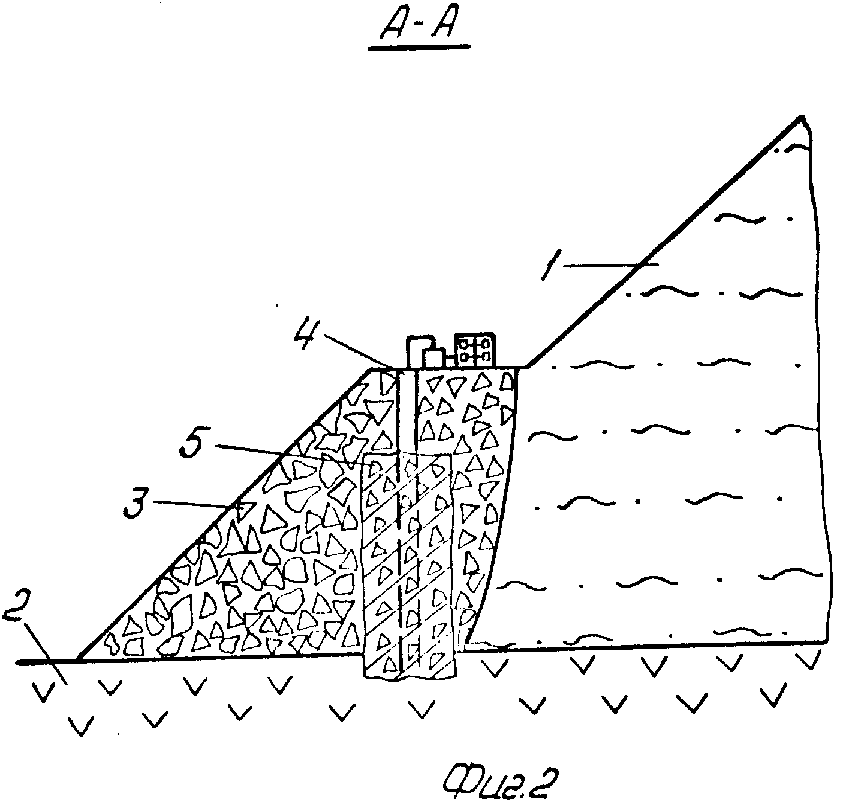 На этом основано применение вибротранспортирующих устройств, вибраторов для облегчения разгрузки бункеров, самосвалов и дозирующих устройств.
На этом основано применение вибротранспортирующих устройств, вибраторов для облегчения разгрузки бункеров, самосвалов и дозирующих устройств.
Знание углов естественного откоса и ссыпания необходимо при проектировании складских помещений, транспортеров, шахтных печей, где имеют дело с сыпучими материалами. Невозможность учета теоретически всех факторов, определяющих величину этих углов, приводит к необходимости экспериментального их определения.
Описание установки. Для определения угла естественного откоса используется гладкая горизонтальная плоскость с нанесенными на ней делениями в сантиметрах и короткий металлический цилиндр; для определения угла ссыпания – прибор, состоящий из вала 1, на который навертывается шнур, кронштейна 2, через который шнур соединяется с подъемной доской 3, и угломера 4,
установленного у оси вращения подъемной доски. Подъемная доска снабжена указателем, показывающим на угломере угол ее подъема (рисунок 3). Для сбора ссыпавшейся массы поставлен ящик.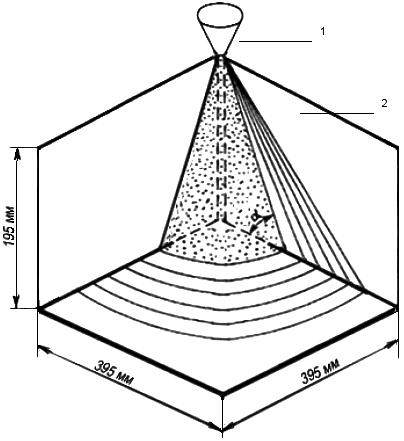 В работе используется также линейка, весы и прямоугольная металлическая рамка.
В работе используется также линейка, весы и прямоугольная металлическая рамка.
Рисунок 3
Проведение опыта и запись наблюдений. При определении углов естественного откоса и ссыпания используется сыпучий материал двух или трех сортов крупности.
А. Определение угла естественного откоса
1. Установить металлический цилиндр в центре горизонтальной плоскости,
2. Набрать совком сыпучий материал и высыпать его в цилиндр.
3. Медленно поднять цилиндр, предоставив материалу свободно рассыпаться по плоскости.
Б. Определение угла ссыпания
1. Уложить на подъемной доске прямоугольную металлическую рамку и полностью засыпать ее сыпучим материалом.
2. Снять прямоугольную рамку и, медленно вращая вал, привести подъемную доску в наклонное положение.
3. Когда материал начнет ссыпаться, прекратить подъем доски и записать угол ее наклона. Перенести весь материал с подъемной доски и ее подставки на лист бумаги, взвесить материал, добавить определенное количество воды (заданное преподавателем), тщательно перемешать и произвести с влажным материалом те же определения (этапы А, 1 – 4 и Б,
Результаты опытов внести в таблицу 2.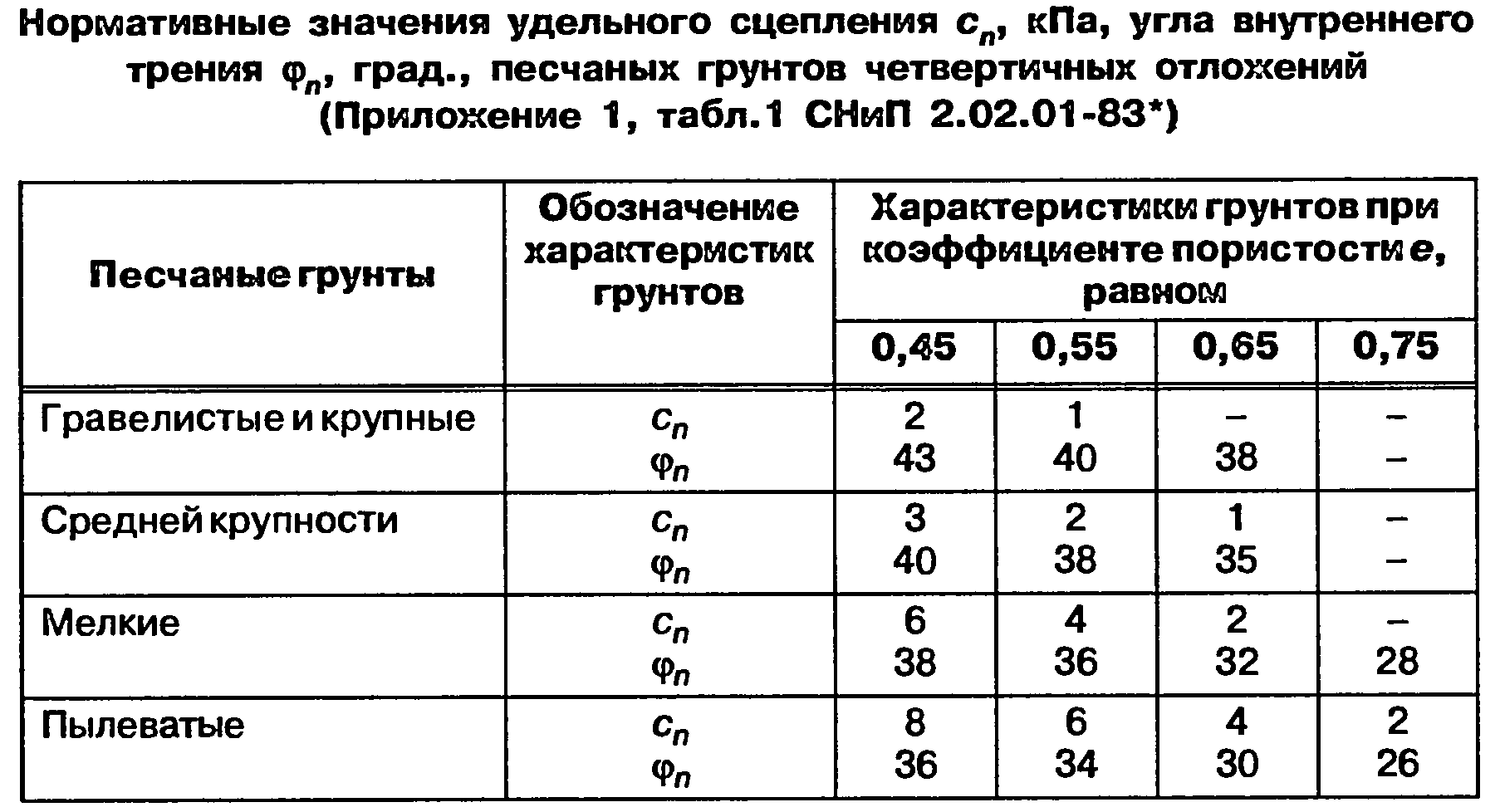
Таблица 2
Наименование исследуемого материала | Угол естественного откоса | Угол ссыпания | ||||||||
сухой материал | влажный материал | Сухой материал | Влажный материал | |||||||
tg α | tg α | |||||||||
Обработка результатов опыта. Пользуясь соотношением определить величину
tg
α
и по таблицам найти соответствующее значение α.
Пользуясь соотношением определить величину
tg
α
и по таблицам найти соответствующее значение α.
font-size:14.0pt; font-family:” times new roman>где α – угол естественного откоса, град.;
Н – высота насыпанной кучи материала, см;
D – диаметр насыпанной кучи материала, см;
font-size:14.0pt; font-family:” times new roman>– радиус насыпанной кучи материала, см,
1) Краткое изложение теории и цель работы.
2) Схема установки.
3) Таблица 2.
4) Вывод по работе.
Задание на подготовку к лабораторной работе .
1) Измельчение твёрдых материалов и их классификация .
2) Измельчение, грохочение и дозирование твёрдых тел .
Контрольные вопросы .
1) Объясните понятие «угол ссыпания».
2) Виды движения кускового материала по плоскости ссыпания.
3) Назовите факторы, от которых зависит величина угла ссыпания зернисто-кускового материала.
4) Объясните понятие «угол естественного откоса зернисто-кускового материала».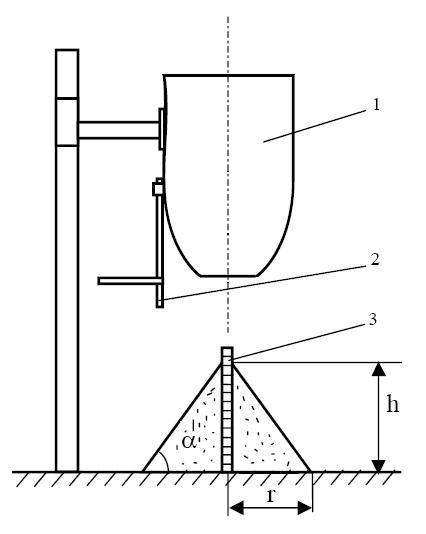
5) Назовите факторы, от которых зависит величина угла естественного откоса.
6) Скажите какая величина больше – угол ссыпания или угол естественного откоса, объясните почему.
7) Как изменяется величина угла ссыпания и угла естественного откоса при движении материала и плоскости, на которой он лежит?
8) Как угол естественного откоса зависит от влажности?
9) тонко или крупно измельчённый материал имеет больший угол естественного откоса?
10) Для чего необходимо знание углов естественного откоса и ссыпания?
Главная
Технико-коммерческое предложениепо предоставлению услуг грунтовой лабораторииАттестованная грунтовая лаборатория предоставляет следующие виды услуг:
Определение физико-механических свойств дисперсных грунтов:
· Гранулометрический состав песчаных и глинистых грунтов:
– гранулометрический (зерновой) состав песчаных грунтов ситовым методом по ГОСТ 12536;
– гранулометрический состав глинистых грунтов ареометрическим методом по ГОСТ 12536.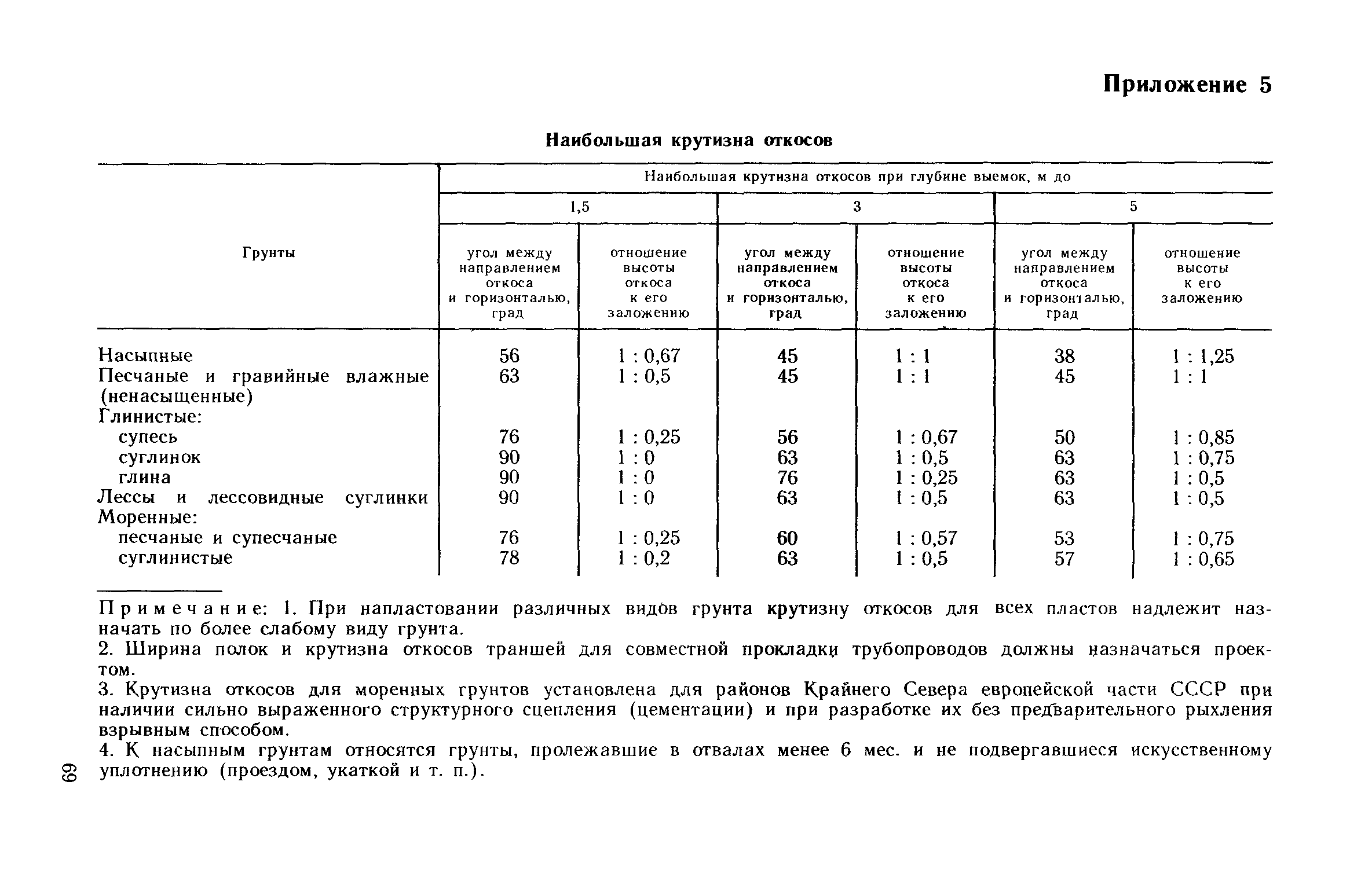
· Влажность:
– методом высушивания грунта до постоянной массы по ГОСТ 5180.
· Плотность:
– методом режущего кольца по ГОСТ 5180;
– методом взвешивания в воде по ГОСТ 5180.
· Плотность частиц грунта:
– определение пикнометрическим методом по ГОСТ 5180.
· Плотность песков в рыхлом и предельно плотном состоянии:
– метод определения по РСН 51-84.
· Угол естественного откоса песков (в сухом состоянии и под водой):
– метод определения по РСН 51-84.
· Коэффициент фильтрации глинистых и песчаных грунтов:
– метод определения по ГОСТ 25584-90.
· Свободное набухание грунта:
– метод определения по ГОСТ 12248.
· Определение максимальной плотности, оптимальной влажности:
– метод определения по ГОСТ 22733.
· Размокаемость грунта:
– метод определения по РСН 51-84.
· Компрессионные испытания:
– метод определения по ГОСТ 12248 (модуль деформации).
· Просадочность:
– метод определения по ГОСТ 23161 (испытание по методу «одной кривой» и «двух кривых»).
· Испытания на сопротивление одноплоскостному срезу:
– метод определения по ГОСТ 12248 (метод консолидированно-дренированный, неконсолидированный быстрый срез).
· Прочностные и деформационные испытания грунтов в условиях трехосного сжатия:
– метод определения по ГОСТ 12248 (метод неконсолидированно-недренированный, консолидированно-недренированный, консолидированно-дренированный).
· Массовая доля органического вещества:
– метод определения по ГОСТ 26213.
· Зольность торфа:
– метод определения по ГОСТ 27784-88.
· Определение степень пучинистости:
– метод определения по ГОСТ 28622
Определение физико-механических свойств скальных грунтов:
· Плотность методом взвешивания в воде:
– по ГОСТ 5180.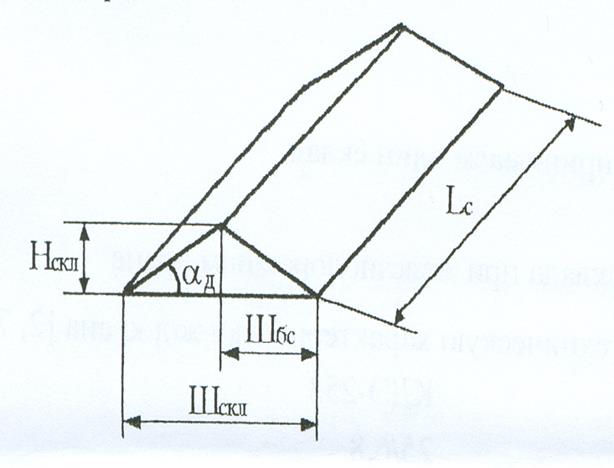
· Предел прочности при одноосном сжатии:
– по ГОСТ 12248.
· Коэффициент размягчаемости;
А так же:
· Коррозионная агрессивность грунта к стали, бетону, алюминию, свинцу;
· Стандартный типовой химический анализ воды;
· Анализ воды на углекислоту агрессивную и спецпробы.
Цена услуг: договорная.
2.106. Кучка песка и самоорганизующийся поток . Новый физический фейерверк
Потихоньку тоненькой струйкой начнем сыпать песок на горизонтальную поверхность. Кучка постепенно приобретет коническую форму. Она будет становиться все выше, а ее основание все шире. Почему угол раствора этого конуса не может превысить некоторое критическое значение?
Медленно перемешайте оранжевый порошок «Тан», из которого делают апельсиновый напиток, и коричневый порошок растворимого чая «Нести». Затем медленно, узкой струйкой высыпьте эту смесь. Как и песок, порошинки образуют кучку. Однако порошок «Нести» собирается на дне кучки. Почему происходит такое разделение?
Однако порошок «Нести» собирается на дне кучки. Почему происходит такое разделение?
Медленно высыпьте смесь «Тана» и «Нести» с одной стороны узкого прозрачного контейнера. Почему при образовании кучки порошинки образуют чередующиеся полосы «Тана» и «Нести» (рис. 2.32)?
Рис. 2.32 / Задача 2.106. Коричневые и оранжевые полосы в кучке порошинок, насыпанных в контейнер.
ОТВЕТ • Когда из сыплющегося песка начинает образовываться коническая кучка, песчинки на склоне конуса сцеплены благодаря трению. Угол наклона поверхности конуса постепенно увеличивается, пока не достигает некоторого критического значения. Затем какие-то песчинки начинают скатываться под уклон вниз, захватывая и другие песчинки, пока на части боковой поверхности конуса не происходит обвал. После этого угол наклона несколько уменьшается и дальше не меняется. Установившийся угол называют углом естественного откоса. Так происходит самоорганизация кучки песка. Это значит, что песок сам «организует» правильную форму — конус с углом наклона, равным углу естественного откоса. Различные пудры и сыпучие материалы (например, бисер, семена, сухой кускус и горох) имеют разные углы естественного откоса, значение которого зависит от формы, коэффициента трения и среднего размера частичек данного материала.
Так происходит самоорганизация кучки песка. Это значит, что песок сам «организует» правильную форму — конус с углом наклона, равным углу естественного откоса. Различные пудры и сыпучие материалы (например, бисер, семена, сухой кускус и горох) имеют разные углы естественного откоса, значение которого зависит от формы, коэффициента трения и среднего размера частичек данного материала.
Если на горизонтальную поверхность сыпать два порошка, предварительно смешав их, то, скатываясь по боковой поверхности кучки, они, вероятно, как-то разделятся и где-то закрепятся. Когда такую смесь насыпают в узкий контейнер, как описано выше, мы видим эту кучку в сечении. Когда начинается обрушение, порошинки большего размера стремятся занять место у основания склона, а скатывающиеся более мелкие порошинки цепляются за поверхность и образуют слой. Затем начинают тормозиться более крупные порошинки, двигающиеся вдоль поверхности, и тоже образуют слой. Итак, ряд обрушений попеременно формирует слои мелких порошинок (в смеси из «Тана» и «Нести» это порошок «Тана») и слои порошинок покрупнее.
Вертикальная стенка из сыпучего материала одновременно и осыпается лавинообразно, и проседает. Чтобы увидеть это, поставьте на стол открытую с двух концов трубку и заполните ее чем-то сыпучим. Затем резко поднимите трубку. Разрушение столбика порошка будет происходить быстро, так что надо следить внимательно либо снять все на скоростную камеру. Образовавшийся столбик разрушится примерно за полсекунды, но то, как это будет происходить, зависит от отношения высоты столбика к его поперечному размеру. Когда это отношение велико, немедленно осыпается вся верхушка столбика и остается горка с закругленной вершиной, а при малых его значениях сначала проседает наружная поверхность столбика, а за ней следует и его внутренняя часть. В результате получается горка с более острой вершиной.
Козырьки и навесы. Наружные и внутренние лестницы. Комплектующие
Лабораторная работа 1. Определение величины угла ссыпания и угла естественного откоса зернисто-кускового материала
Определение величины угла ссыпания и угла естественного откоса зернисто-кускового материала
Цель работы. Определить величины угла естественного откоса и угла ссыпания зернисто-кускового материала.
Теоретические положения . Зернисто-кусковой материал, лежащий на наклонной плоскости (например, на наклонной плоскости бункера , на наклонном ленточном транспортере и т. д.), при определенном угле наклона этой плоскости к горизонту начинает ссыпаться по ней. Такой предельный угол наклона называется углом ссыпания.
В зависимости от формы кусочков можно наблюдать два вида движения кускового материала по плоскости ссыпания: скольжение и перекатывание. Скольжение наблюдается при кусках с развитыми плоскими гранями; передвижению кусков здесь препятствует трение скольжения между гранями кусков и плоскостью ссыпания. Качение наблюдается при форме кусков, близкой к шару. В этом случае передвижение куска происходит как скатывание его, с сопротивлением трения качения.
Предельное состояние покоя слоя кускового материала на наклонной плоскости имеет место тогда, когда сила трения F равна проекции М силы тяжести G на эту плоскость (рисунок 1). С другой стороны, эта же сила трения пропорциональна нормальному давлению кускового материала на наклонную плоскость
F = M = fN ,
откуда f = М / N = tgα
где f – коэффициент трения, определяемый свойствами самого материала, равный tga ;
α – угол ссыпания зернисто-кускового материала.
Рисунок 1
Если рассматривать весь слой сыпучего материала , который перемещается по гладкой наклонной плоскости, то здесь, даже в случае кусков шарообразной формы, происходит скорее скольжение материала по плоскости, чем перекатывание, так как весь материал «течет» сплошной массой.
Угол ссыпания зависит от коэффициента трения материала о плоскость ссыпания, от формы и крупности кусков, от структуры поверхности, по которой происходит ссыпание (поверхность может быть гладкой, шероховатой, ребристой и т. д.), а также он влажности самого кускового материала.
д.), а также он влажности самого кускового материала.
Если насыпать зернисто-кусковой материал на горизонтальную плоскость, то он располагается на ней в виде конуса. Угол между образующей этого конуса и горизонтальной плоскостью называется углом естественного откоса зернисто-кускового материала.
Угол естественного откоса всегда больше угла ссыпания (для одного и того же материала), так как наличие неровностей на поверхности материала препятствует скатыванию, а тем более скольжению кусков. Угол естественного откоса в большой степени зависит от фракционного состава кускового материала, ибо последний определяет собой общую структуру поверхности конуса. Эта разнородность размера кусков вызывает в то же время преимущественное скатывание крупных кусков материала на край насыпаемой кучи, вследствие того, что неровности поверхности оказывают меньшее сопротивление перекатыванию крупн
ых кусков, чем мелких (рисунок 2). Неравномерное распределение кусков по крупности необходимо учитывать при загрузке насадочных абсорберов, шахтных печей и т.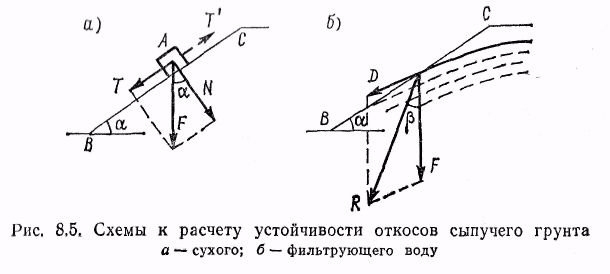 д., так как в местах расположения крупных кусков, т. е. на-периферии, получается большее сечение каналов и газ пойдет преимущественно по этим каналам, имеющим меньшее гидравлическое сопротивление.
д., так как в местах расположения крупных кусков, т. е. на-периферии, получается большее сечение каналов и газ пойдет преимущественно по этим каналам, имеющим меньшее гидравлическое сопротивление.
Тонко измельченные материалы имеют больший угол естественного откоса, т. е. меньшую сыпучесть, в связи с более развитой поверхностью трения.
Рисунок 2
Угол естественного откоса значительно зависит от влажности материала, потому что вода, располагаясь на поверхности кусков, вызывает слипание их и тем самым затрудняет движение отдельных кусков. Чем меньше куски материала, тем больше проявляется влияние влажности; но чрезмерное увлажнение приводит к увеличению послойной текучести жидкости между кусочками материала, и угол естественного откоса вновь уменьшается (таблица 1).
Таблица 1
Порода | Угол естественного откоса, град, для породы | ||
сухой | влажной | мокрой | |
Песок крупный | 30 – 35 | 32 – 40 | 25 – 27 |
Песок средний | 28 – 30 | ||
Песок мелкий | 30 – 35 | 15 – 20 | |
Гравий | 35 – 40 |
Угол естественного откоса и угол ссыпания резко уменьшаются при движении материала и плоскости, на которой он лежит.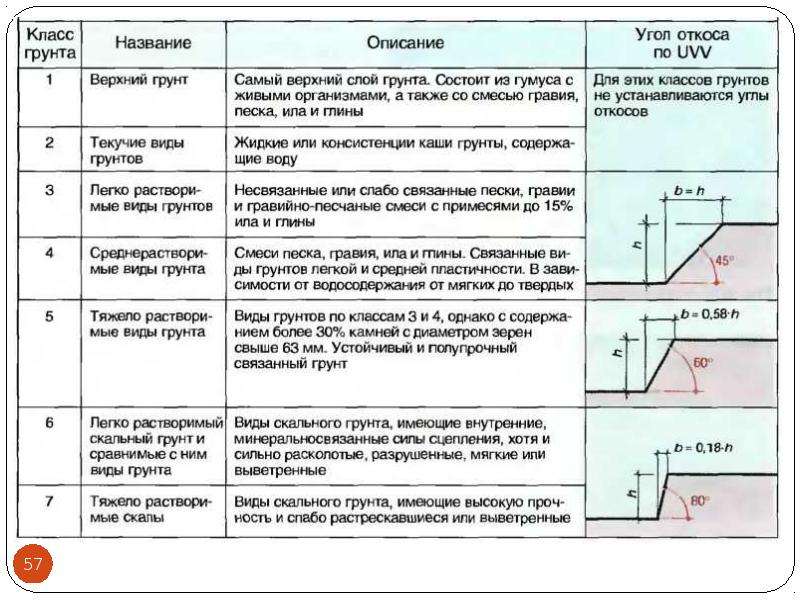 При сотрясениях или вибрациях материал интенсивно рассыпается, растекается, стремясь принять горизонтальное положение, так как при вибрациях в отдельные моменты уменьшается взаимное трение по поверхности соприкосновения кусочков друг с другом и кусочков с плоскостью. На этом основано применение вибротранспортирующих устройств, вибраторов для облегчения разгрузки бункеров, самосвалов и дозирующих устройств.
При сотрясениях или вибрациях материал интенсивно рассыпается, растекается, стремясь принять горизонтальное положение, так как при вибрациях в отдельные моменты уменьшается взаимное трение по поверхности соприкосновения кусочков друг с другом и кусочков с плоскостью. На этом основано применение вибротранспортирующих устройств, вибраторов для облегчения разгрузки бункеров, самосвалов и дозирующих устройств.
Знание углов естественного откоса и ссыпания необходимо при проектировании складских помещений, транспортеров, шахтных печей, где имеют дело с сыпучими материалами. Невозможность учета теоретически всех факторов, определяющих величину этих углов, приводит к необходимости экспериментального их определения.
Описание установки. Для определения угла естественного откоса используется гладкая горизонтальная плоскость с нанесенными на ней делениями в сантиметрах и короткий металлический цилиндр; для определения угла ссыпания – прибор, состоящий из вала 1, на который навертывается шнур, кронштейна 2, через который шнур соединяется с подъемной доской 3, и угломера 4,
установленного у оси вращения подъемной доски.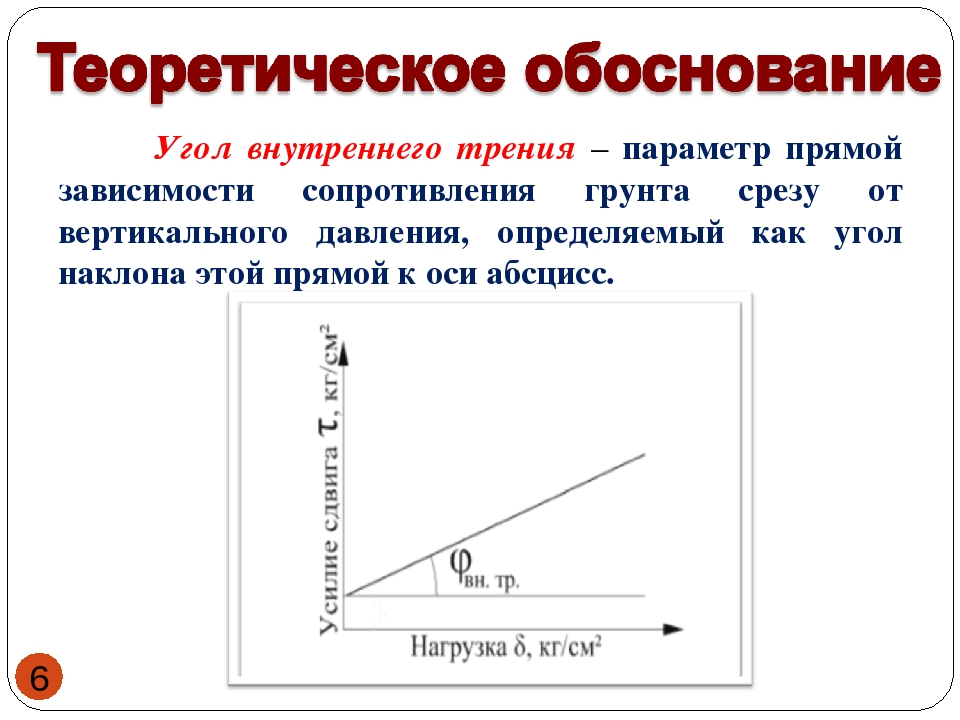 Подъемная доска снабжена указателем, показывающим на угломере угол ее подъема (рисунок 3). Для сбора ссыпавшейся массы поставлен ящик. В работе используется также линейка, весы и прямоугольная металлическая рамка.
Подъемная доска снабжена указателем, показывающим на угломере угол ее подъема (рисунок 3). Для сбора ссыпавшейся массы поставлен ящик. В работе используется также линейка, весы и прямоугольная металлическая рамка.
Рисунок 3
Проведение опыта и запись наблюдений. При определении углов естественного откоса и ссыпания используется сыпучий материал двух или трех сортов крупности.
А. Определение угла естественного откоса
1. Установить металлический цилиндр в центре горизонтальной плоскости,
2. Набрать совком сыпучий материал и высыпать его в цилиндр.
3. Медленно поднять цилиндр, предоставив материалу свободно рассыпаться по плоскости.
Б. Определение угла ссыпания
1. Уложить на подъемной доске прямоугольную металлическую рамку и полностью засыпать ее сыпучим материалом.
2. Снять прямоугольную рамку и, медленно вращая вал, привести подъемную доску в наклонное положение.
3. Когда материал начнет ссыпаться, прекратить подъем доски и записать угол ее наклона. Перенести весь материал с подъемной доски и ее подставки на лист бумаги, взвесить материал, добавить определенное количество воды (заданное преподавателем), тщательно перемешать и произвести с влажным материалом те же определения (этапы А, 1 – 4 и Б,
Когда материал начнет ссыпаться, прекратить подъем доски и записать угол ее наклона. Перенести весь материал с подъемной доски и ее подставки на лист бумаги, взвесить материал, добавить определенное количество воды (заданное преподавателем), тщательно перемешать и произвести с влажным материалом те же определения (этапы А, 1 – 4 и Б,
Результаты опытов внести в таблицу 2.
Таблица 2
Наименование исследуемого материала | Угол естественного откоса | Угол ссыпания | ||||||||
сухой материал | влажный материал | Сухой материал | Влажный материал | |||||||
tg α | tg α | |||||||||
Обработка результатов опыта.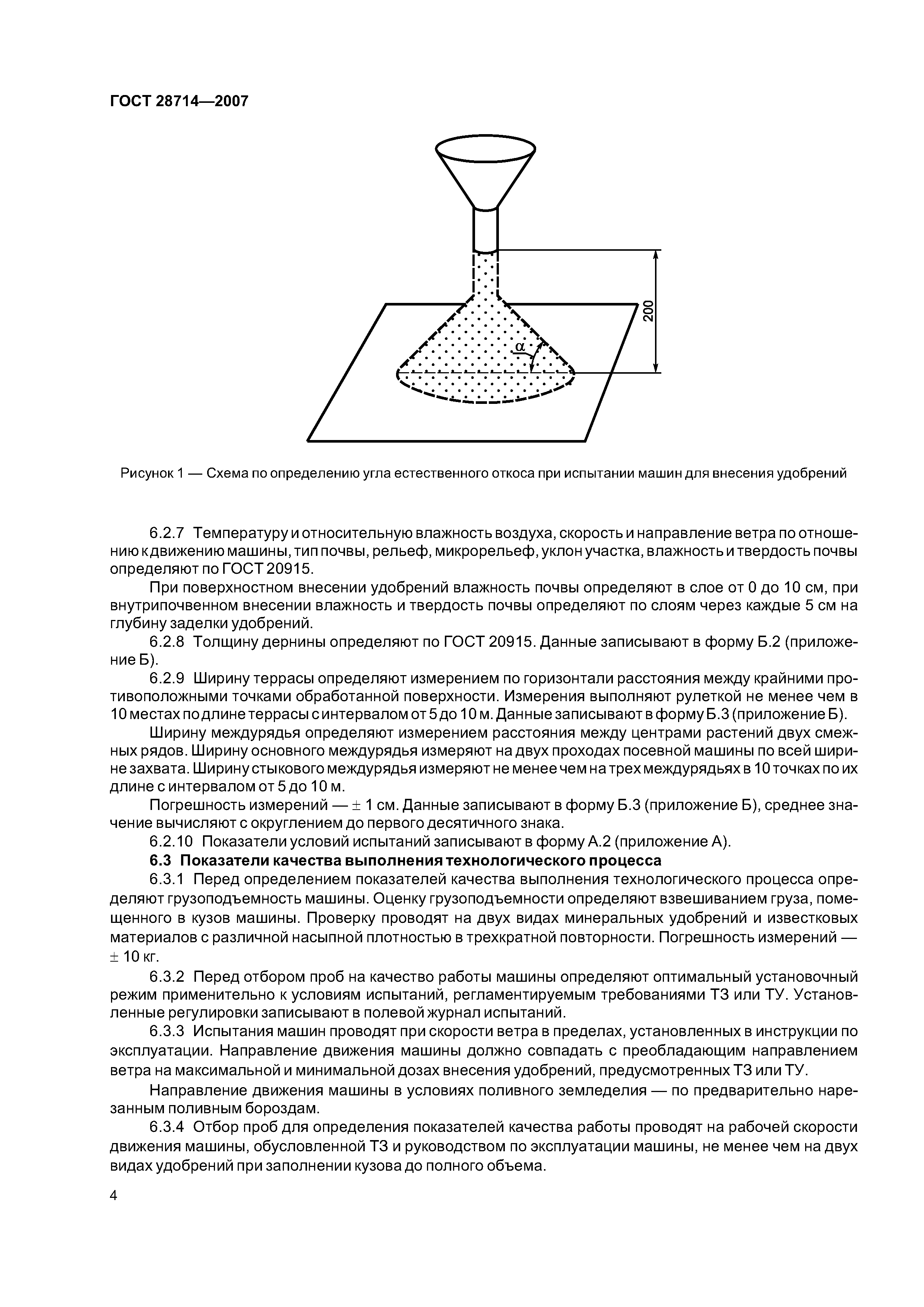 Пользуясь соотношением определить величину
tg
α
и по таблицам найти соответствующее значение α.
Пользуясь соотношением определить величину
tg
α
и по таблицам найти соответствующее значение α.
font-size:14.0pt; font-family:” times new roman>где α – угол естественного откоса, град.;
Н – высота насыпанной кучи материала, см;
D – диаметр насыпанной кучи материала, см;
font-size:14.0pt; font-family:” times new roman>– радиус насыпанной кучи материала, см,
1) Краткое изложение теории и цель работы.
2) Схема установки.
3) Таблица 2.
4) Вывод по работе.
Задание на подготовку к лабораторной работе .
1) Измельчение твёрдых материалов и их классификация .
2) Измельчение, грохочение и дозирование твёрдых тел .
Контрольные вопросы .
1) Объясните понятие «угол ссыпания».
2) Виды движения кускового материала по плоскости ссыпания.
3) Назовите факторы, от которых зависит величина угла ссыпания зернисто-кускового материала.
4) Объясните понятие «угол естественного откоса зернисто-кускового материала».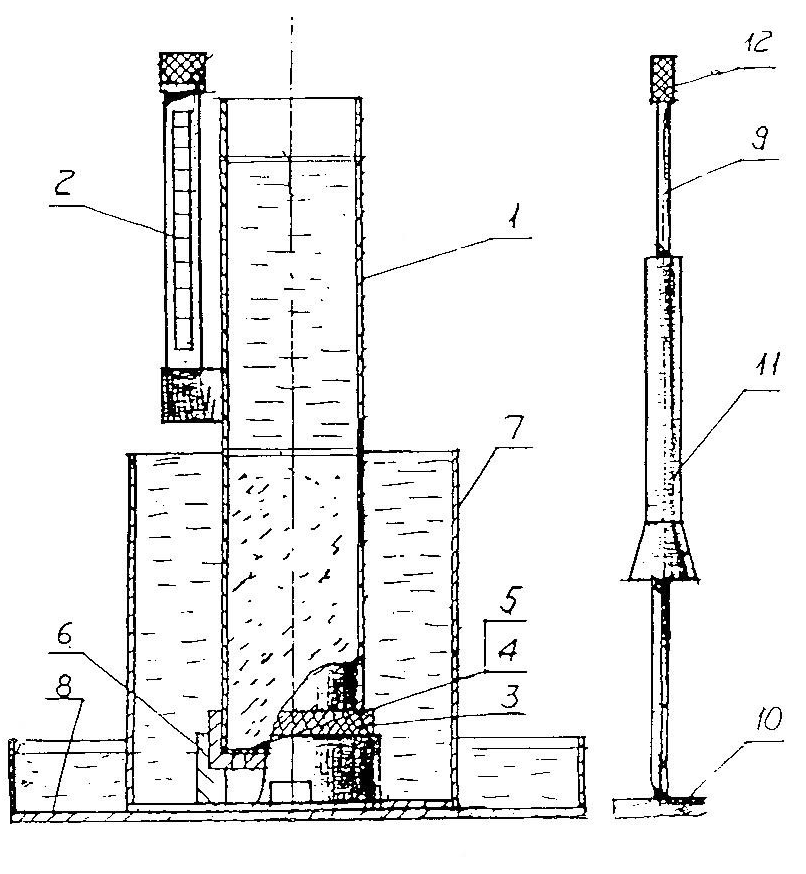
5) Назовите факторы, от которых зависит величина угла естественного откоса.
6) Скажите какая величина больше – угол ссыпания или угол естественного откоса, объясните почему.
7) Как изменяется величина угла ссыпания и угла естественного откоса при движении материала и плоскости, на которой он лежит?
8) Как угол естественного откоса зависит от влажности?
9) тонко или крупно измельчённый материал имеет больший угол естественного откоса?
10) Для чего необходимо знание углов естественного откоса и ссыпания?
Цель работы :
Определить угол естественного откоса испытуемого грунта в лабораторных условиях в сухом состоянии и под водой.
Сущность метода:
Угол естественного откоса песков – это предельный угол свободного отсыпания песка, при котором грунтовая масса находится в устойчивом состоянии. Этот показатель определяется как в сухом состоянии, так и под водой.
Угол естественного откоса испытуемого грунта определяется в лабораторных условиях прибором для определения угла естественного откоса, входящим в состав полевой лаборатории Литвинова ПЛЛ-9.
Угол естественного откоса песка в сухом состоянии равен углу внутреннего трения этого песка
Оборудование:
Прибор для определения угла естественного откоса;
Воронка;
Нож с прямым лезвием;
Мерный сосуд.
Рис.5. Прибор для определения угла естественного откоса песков
1- выдвижная створка;
2- малое отделение.
Определение угла естественного откоса песков в сухом состоянии
Порядок работы:
3. Песок разровнять ножом.
4. После этого постепенно поднимают выдвижную створку, следя, чтобы не было толчков; при этом прибор придерживают рукой.
5. Песок частично пересыпается в другое отделение, пока не наступает положение устойчивого равновесия; угол между плоскостью свободного откоса и горизонтальной плоскостью и есть угол естественного откоса.
6. По делениям на днище и боковой стенке отсчитывают высоту и заложение откоса и вычисляют тангенс угла естественного откоса. Отсчеты ведут с точностью 1 мм.
Отсчеты ведут с точностью 1 мм.
7. Испытания проводят два раза.
8. Числовое значение тангенса угла естественного откоса определяется как среднее арифметическое из результатов двух замеров.
9. Результаты определений заносят в таблицу 5.
Определение угла естественного откоса песков в подводном состоянии
Порядок работы:
1. Прибор ставят на стол или иную горизонтальную поверхность. Выдвижная створка при этом опущена до дна.
2. В малое отделение прибора насыпают песок небольшими порциями через воронку вровень с краями.
3. Песок разровнять ножом.
4. После того, как в малое отделение прибора насыпан испытываемый грунт, в большое отделение наливают доверху воду.
5. После этого выдвижную створку поднимают на несколько миллиметров, чтобы вода могла проникнуть в малое отделение.
6. Когда грунт пропитается водой, постепенно поднимают выдвижную створку, следя, чтобы не было толчков; при этом прибор придерживают рукой.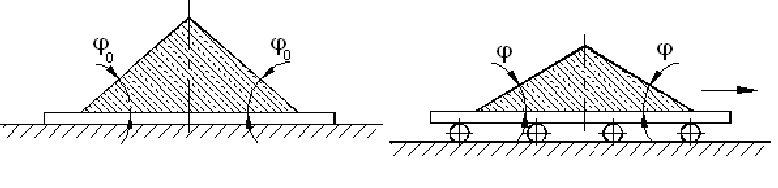
7. Песок частично пересыпается в другое отделение, пока не наступает положение устойчивого равновесия; угол между плоскостью свободного откоса и горизонтальной плоскостью и есть угол естественного откоса.
8. По делениям на днище и боковой стенке отсчитывают высоту и заложение откоса и вычисляют тангенс угла естественного откоса. Отсчеты ведут с точностью 1 мм.
9. Испытания проводят два раза.
10. Числовое значение тангенса угла естественного откоса определяется как среднее арифметическое из результатов двух замеров.
11. Результаты определений заносят в таблицу 5.
Таблица 5 Результаты определений угла естественного откоса.
Лабораторная работа № 6
Определение коэффициента фильтрации песчаного грунта
Цель работы:
Определить коэффициент фильтрации испытуемого песчаного грунта в лабораторных условиях.
Сущность метода:
Коэффициент фильтрации К ф – это численная характеристика водопроницаемости (способности грунта фильтровать воду).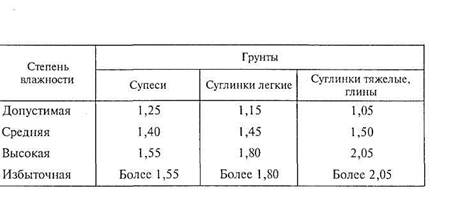 Он представляет собой скорость фильтрации и выражается обычно в см/с или в м/сут.
Он представляет собой скорость фильтрации и выражается обычно в см/с или в м/сут.
Коэффициент фильтрации определяется на грунтах нарушенного сложения при оптимальной влажности и максимальной стандартной плотности, значения которых предварительно определяются в лабораторной работе №4.
Коэффициент фильтрациииспользуется при подсчете запасов подземных вод, определении притока воды в строительные котлованы и горные выработки, при расчете утечек воды из водохранилищ, проектировании дренажных сооружений и фильтров, а так же в ряде других расчетов.
В настоящей лабораторной работе установлен порядок определения коэффициента фильтрации песчаных грунтов и строительных песков, применяемых в строительстве.
Оборудование:
Прибор Союздорнии ПКФ-СД;
Весы с точностью 0.01 г.;
Чашки металлические емкостью не менее 5 л;
Цилиндры мерные с носиком емкостью 100 и 500 мл;
Лопаточка – мастерок;
Линейка металлическая длиной 30 см;
Секундомер;
Термометр;
Резиновая груша.
Рис 6. Общий вид прибора ПКФ-СДдля определения коэффициента фильтрации.
1- рабочий цилиндр; 2- пьезометр; 3- перфорированное дно;
10- наковальня; 11-ударник; 12-рукоятка.
Прибор состоит из следующих основных частей: фильтрационной трубки в сборе, загрузочной воронки, подставки, трамбующего устройства, стакана, и ванны.
Фильтрационная трубка в сборе включает рабочий цилиндр 1, на котором размещен пьезометр 2. Снизу к цилиндру навинчено перфорированное дно 3 с сеткой 4. После уплотнения грунта фильтрационная трубка устанавливается на подставку 6. Трамбующее устройство состоит из направляющего стержня 9, наковальни 10, ударника 11 массой 500 гр и рукоятки 12.
Для проведения опыта по определению коэффициента фильтрации К ф при гидравлическом градиенте i=1, фильтрационная трубка с подставкой помещается в стакан 7. При гидравлическом градиенте i=2 , фильтрационная трубка с подставкой помещается непосредственно в ванну 8.
Порядок работы:
Формирование образца
1. Засыпать в рабочий цилиндр первую навеску, вставить в него трамбовку (масса груза 0,5кг, высота падения груза 0,3м), провести 40 ударов по уплотняемому грунту.
2. Замерить с помощью линейки с точностью до 1мм в трех точках расстояние от поверхности уплотненного грунта до верха цилиндра. Результаты замеров записать в таблицу 6.2 и определить среднее значение.
3. Взрыхлить поверхность уплотненного слоя ножом на глубину 1-2мм. Засыпать в рабочий цилиндр вторую навеску, повторить уплотнение образца и замерить расстояние от поверхности уплотненного грунта до верха цилиндра. Результаты замеров записать в таблицу 6.2 и определить среднее значение.
4. Засыпать в рабочий цилиндр третью навеску, повторить операции по уплотнению, проведению замеров. Записать результаты в таблицу 6.2 и определить среднее значение.
5. После завершения операций уплотнения грунта рабочий цилиндр с грунтом взвесить с точностью до 1гр.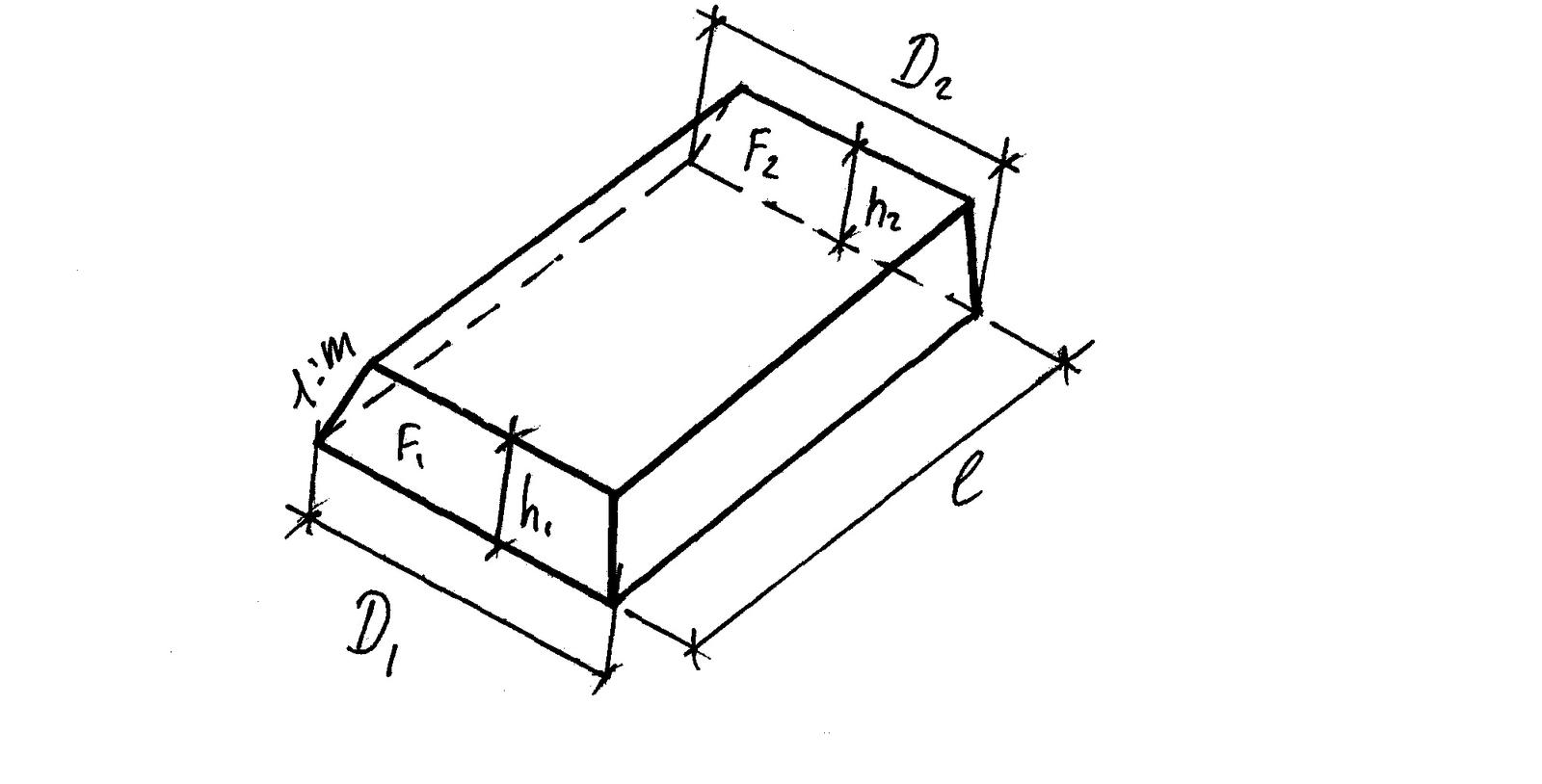 Результаты взвешивания занести в таблицу 6.2.
Результаты взвешивания занести в таблицу 6.2.
6. На поверхность уплотненного грунта в рабочем цилиндре засыпать гравий с размером частиц 2-5мм таким образом, чтобы толщина слоя гравия составила 5-10мм.
Насыщение образца водой.
1. Фильтрационную трубку с уплотненным грунтом поместить во входящий в комплект прибора металлический стакан 7, высота которого соответствует верхнему уровню грунта в рабочем цилиндре. Заполнить этот стакан водой на 2/3 высоты и выдержать перед проведением следующей операции в течении 15 минут.
2. Перенести стакан с помещенной в него фильтрационной трубкой в резервуар с водой емкостью 8-10 литров и довести уровень воды в этом резервуаре до высоты на 10-15 мм выше верхней кромки стакана.
3. Выдержать стакан в резервуаре с водой до появления зеркала воды над слоем гравия и зафиксировать время насыщения грунта водой в таблицу 6.2.
Проведение испытаний.
1. Осторожно долить воду во внутреннюю полость фильтрационной трубки на 1/3 её высоты и перенести прибор вместе с металлическим стаканом в ванну для проведения замеров длительности фильтрации, расположив ее таким образом, чтобы нулевая отметка водомерной трубки располагалась на уровне глаз.
2. Долить во внутреннюю полость фильтрационной трубки воду до уровня, превышающего не менее, чем на 0,5см нулевую отметку водомерной трубки (каждое деление на водомерной трубке соответствует 0,5см).
3. Проверить уровень воды в металлическом стакане и, в случае необходимости, заполнить его водой до верху.
4. Установить в металлический стакан термометр для измерения температуры воды в процессе испытания.
5. Провести первый замер длительности фильтрации по секундомеру, включить последний в момент, когда уровень воды в водомерной трубке достигнет нулевого деления, и выключить, когда он установится на отметке 5см, и зарегистрировать при этом температуру воды. Уровень воды в фильтрационной трубке в процессе испытания не должен отпускаться ниже поверхности слоя гравия.
6. В случае, если длительность фильтрации превышает 2 минуты, второй замер провести при падении уровня воды до отметки 2см. В противном случае все последующие замеры проводить при падении уровня до отметки 5см, во всех случаях регистрируя потерю воды.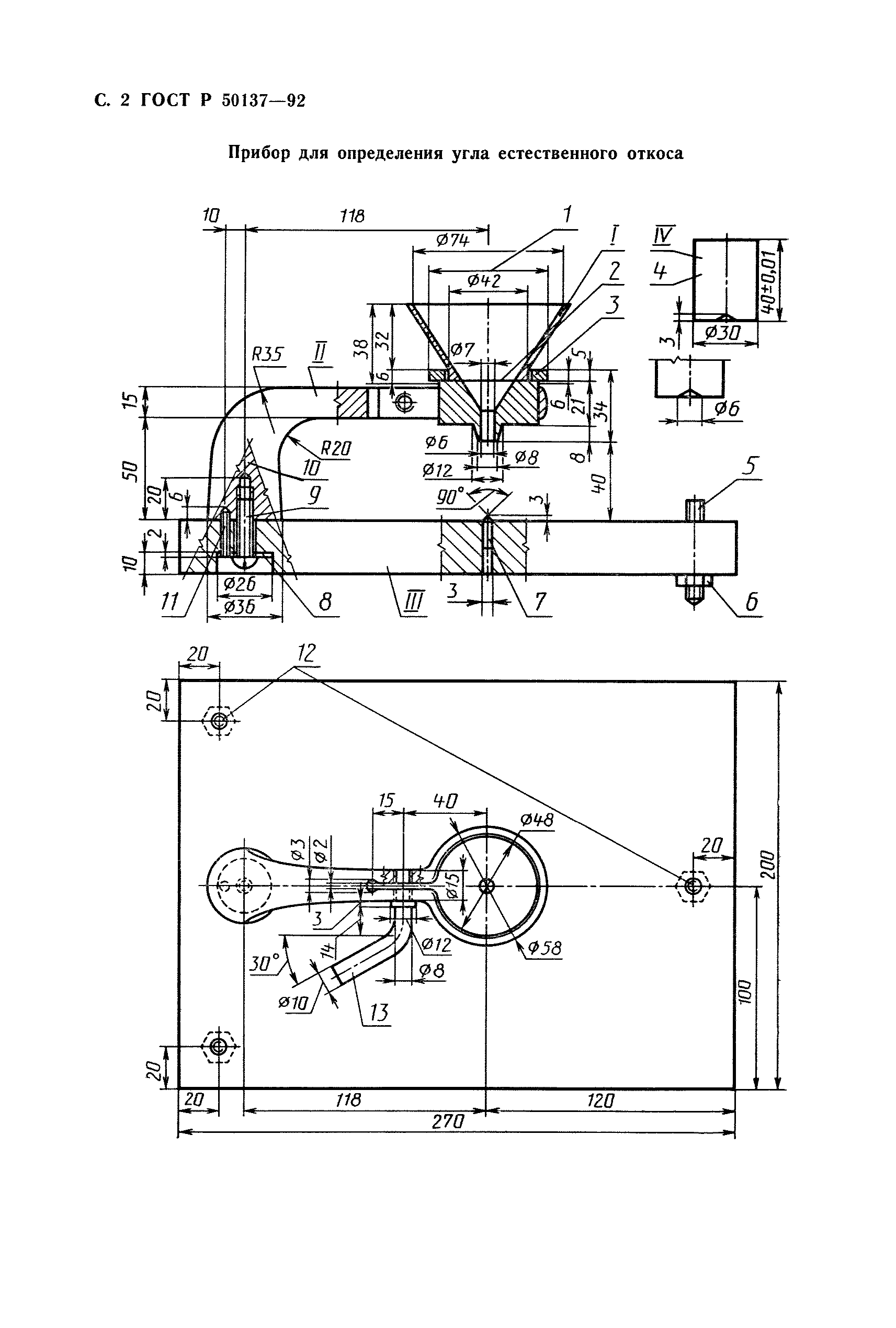 Уровень воды в фильтрационной трубке в процессе испытания не должен отпускаться ниже поверхности слоя гравия.
Уровень воды в фильтрационной трубке в процессе испытания не должен отпускаться ниже поверхности слоя гравия.
7. В случае, если длительность фильтрации по предыдущему пункту превышает две минуты, все последующие замеры проводить при падении уровня воды до отметки 1см. В противном случае все последующие замеры проводить при падении уровня до отметки 2см, во всех случаях регистрируя температуру воды. Уровень воды в фильтрационной трубке в процессе испытаний не должен отпускаться ниже поверхности слоя гравия.
8. В случае, если длительность фильтрации по предыдущему пункту превышает 10 минут, градиент напора при проведении испытания необходимо принять равным 2. Для этого фильтрационную трубку вместе с подставкой необходимо извлечь из металлического стакана и установить ее в ванну без стакана.
9. Результаты каждого измерения и регистрируемую в его процессе температуру воды занести в таблицу 6.2.
Обработка результатов:
где K 10 – коэффициент фильтрации, м/сут;
I – высота фильтрующего слоя песка, определяемая, как разность между общей высотой фильтрационной трубки Н о и расстоянием от верхнего торца трубки до поверхности грунта h 3 , см.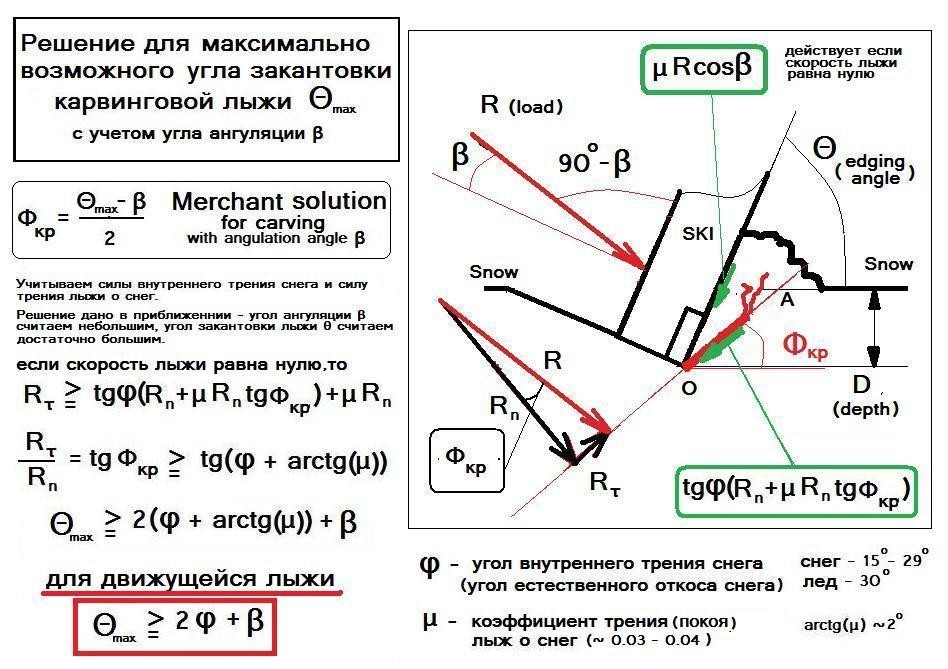
t m – средняя продолжительность фильтрации, сек;
Т ср – температура воды, ˚С;
Значение функции падения уровня воды, определяемое по таблице 6.1;
S – падение уровня воды в водомерной трубке, см;
h o – высота первоначального напора воды в приборе от его дна до нулевого деления водомерной трубки, равная 10 для градиента напора 1 или 20 для градиента напора 2.
2. Занести полученные значения в таблицу 6.2 с округлением результатов до 0,1м/сут, если величина коэффициента фильтрации составляет менее 5м/сут, и округлением результатов до целых чисел, если коэффициент фильтрации более 5м/сут.
3. После проведения расчетов сравнить полученные результаты с усредненными значениями коэффициента фильтрации различных типов грунтов:
Галечник чистый ……………………………более 100 м/сут;
Галечник с песчаным заполнителем..………100-200 м/сут;
Пески чистые разной крупности ……………50-2 м/сут;
Пески глинистые, супеси…………….………2-0,1 м/сут;
Суглинки ………………………….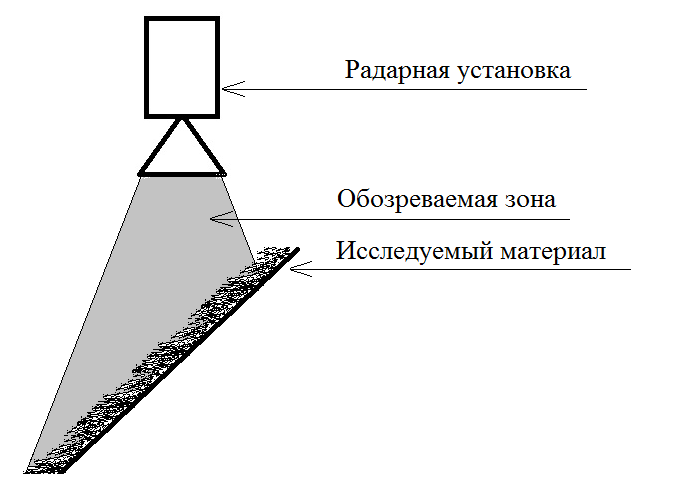 ..…………менее 0,1 м/сут;
..…………менее 0,1 м/сут;
Глины …………………………………………..менее 0,01 м/сут.
Таблица 6.1. Зависимость величины падения уровня воды от первоначального напора.
| S/h 0 | φ(S/h 0) | S/h 0 | φ(S/h 0) | S/h 0 | φ(S/h 0) | S/h 0 | φ(S/h 0) |
| 0,01 | 0,010 | 0,26 | 0,301 | 0,51 | 0,713 | 0,76 | 1,427 |
| 0,02 | 0,020 | 0,27 | 0,315 | 0,52 | 0,734 | 0,77 | 1,470 |
| 0,03 | 0,030 | 0,28 | 0,329 | 0,53 | 0,755 | 0,78 | 1,514 |
| 0,04 | 0,040 | 0,29 | 0,346 | 0,54 | 0,777 | 0,79 | 1,561 |
| 0,05 | 0,051 | 0,3 | 0,357 | 0,55 | 0,799 | 0,8 | 1,609 |
| 0,06 | 0,062 | 0,31 | 0,371 | 0,56 | 0,821 | 0,81 | 1,661 |
| 0,07 | 0,073 | 0,32 | 0,385 | 0,57 | 0,844 | 0,82 | 1,715 |
| 0,08 | 0,083 | 0,33 | 0,400 | 0,58 | 0,863 | 0,83 | 1,771 |
| 0,09 | 0,094 | 0,34 | 0,416 | 0,59 | 0,892 | 0,84 | 1,838 |
| 0,1 | 0,105 | 0,35 | 0,431 | 0,6 | 0,916 | 0,85 | 1,897 |
| 0,11 | 0,117 | 0,36 | 0,446 | 0,61 | 0,941 | 0,86 | 1,966 |
| 0,12 | 0,128 | 0,37 | 0,462 | 0,62 | 0,957 | 0,87 | 2,040 |
| 0,13 | 0,139 | 0,38 | 0,478 | 0,63 | 0,994 | 0,88 | 2,120 |
| 0,14 | 0,151 | 0,39 | 0,494 | 0,64 | 1,022 | 0,89 | 2,207 |
| 0,15 | 0,163 | 0,4 | 0,510 | 0,65 | 1,050 | 0,9 | 2,303 |
| 0,16 | 0,174 | 0,41 | 0,527 | 0,66 | 1,079 | 0,91 | 2,408 |
| 0,17 | 0,186 | 0,42 | 0,545 | 0,67 | 1,109 | 0,92 | 2,526 |
| 0,18 | 0,196 | 0,43 | 0,562 | 0,68 | 1,139 | 0,93 | 2,659 |
| 0,19 | 0,210 | 0,44 | 0,580 | 0,69 | 1,172 | 0,94 | 2,813 |
| 0,2 | 0,223 | 0,45 | 0,593 | 0,7 | 1,204 | 0,95 | 2,996 |
| 0,21 | 0,236 | 0,46 | 0,616 | 0,71 | 1,238 | 0,96 | 3,219 |
| 0,22 | 0,248 | 0,47 | 0,635 | 0,72 | 1,273 | 0,97 | 3,507 |
| 0,23 | 0,261 | 0,48 | 0,654 | 0,73 | 1,309 | 0,98 | 3,912 |
| 0,24 | 0,274 | 0,49 | 0,673 | 0,74 | 1,347 | 0,99 | 4,605 |
| 0,25 | 0,288 | 0,5 | 0,693 | 0,75 | 1,386 | – | – |
Таблица 6. 2. Результаты определения коэффициента фильтрации.
2. Результаты определения коэффициента фильтрации.
| оп. | Влажность грунта, W, % | Масса, гр. | Высота фильтрационной трубки, см. | Плотность грунта, г/см 3 | Время фильтрации, сек. | Падение уровня воды в трубке, см. | Температура воды, ˚С | Градиент напора | Коэффициент фильтрации, м/сут. | ||||||
| Цилиндра | цилиндра с грунтом | грунта | Начальная, h 0 . | Над уплотненным образцом грунта, h 3. | Влажного | Сухого | Отдельного замера | Среднее значение | Отдельного замера | Среднее значение | |||||
Измерение длительности фильтрации при выбранных уровнях падения воды и градиенте напора следует провести не менее 2 раз, рассчитав после этого среднее значение.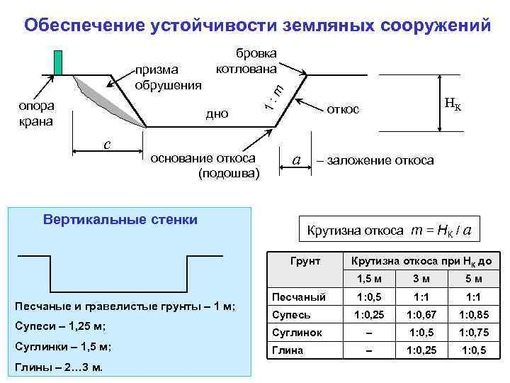
Лабораторная работа №7
Углом естественного откоса грунта называется наибольшее значение угла, который образует с горизонтальной плоскостью поверхность грунта, отсыпанного без толчков; сотрясений и колебаний.
Угол естественного откоса зависит от сопротивления грунта сдвигу. Для установления этой зависимости представим себе грунтовое тело, рассеченное плоскостью а – а, наклоненной к горизонту под углом а (рис. 22).
Часть грунта выше плоскости а – а, рассматриваемая как единый массив, может оставаться в покое или прийти в движение под действием силы P – собственного веса и воздействия возведенного на нем сооружения.
Разложим P на две силы: N = P cos а, направленную нормально к плоскости а – а и силу T = P sin а, параллельную плоскости а – а. Сила T стремится сдвинуть отсеченную часть, которая удерживается силами сцепления и трения в плоскости а – а.
В состоянии предельного равновесия, когда сдвигающая сила уравновешивается сопротивлением трения и сцепления, но когда сдвига еще нет, выполняется равенство 26, т. е. T = N tg ф + CF.
е. T = N tg ф + CF.
В глинистых грунтах сдвигу в основном противодействует сцепление.
В сухом песке сцепления почти нет и состояние предельного равновесия характеризуется соотношением T = N tg ф. Подставляя значения N и T, получим P sin а = P cos a tg ф или tg a = tg ф и а = ф, т. е. угол а соответствует углу внутреннего трения грунта ф в состоянии предельного равновесия массива несвязного грунта.
Определение угла естественного откоса песка показано на рис. 23. Угол естественного откоса песка определяют дважды – для состояния естественной влажности и под водой. Для этого в стеклянный прямоугольный сосуд насыпают песчаный грунт, как показано на рис. 23, а. Затем сосуд наклоняют под углом не менее 45° и осторожно возвращают в прежнее положение (рис. 23, б). Далее определяется угол а между образовавшимся откосом песчаного грунта и горизонталью; о величине угла а можно судить по отношению hl, равному tg а.
В последние годы для определения характеристик сопротивления грунтов сдвигу предложен ряд новых методов: по данным испытания грунтов в стабилометрах (см.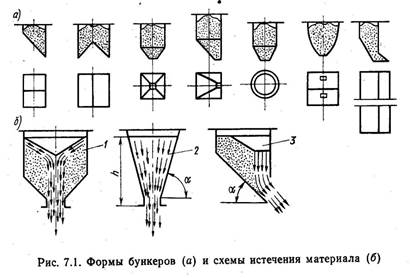 рис. 11), по вдавливанию шарикового штампа в грунт (рис. 24), аналогично определению твердости по Бринеллю и др.
рис. 11), по вдавливанию шарикового штампа в грунт (рис. 24), аналогично определению твердости по Бринеллю и др.
Испытание грунта методом шариковой пробы (рис. 24) заключается в измерении осадки шарика S при действии на него постоянной нагрузки р.
Значение эквивалентного сцепления грунта определяется по следующей формуле:
где P – полная нагрузка на
D – диаметр шарика, см;
S – осадка шарика, см.
Величина сцепления сш учитывает не только силы сцепления грунта, но и внутреннее трение.
Для определения удельного сцепления с значение сш умножается на коэффициент К, который зависит от угла внутреннего трения ф (град).
В последние годы метод шариковой пробы стали применять в полевых условиях. В этом случае применяются полусферические штампы размером до 1 м (рис. 25).
Характеристики сдвига ф и с называются прочностными и точность их определения имеет большое значение при расчете оснований сооружений по прочности и устойчивости.
Угол естественного откоса – это наибольший угол, который
может быть образован откосом свободно насыпанного грунта в
состоянии равновесия с горизонтальной плоскостью.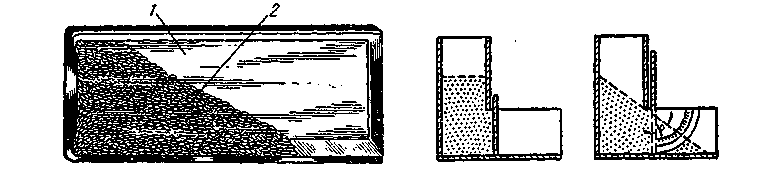
Угол естественного откоса зависит от гранулометрического состава и формы
частиц. С уменьшением размера зерен угол естественного откоса становится
положе.
В воздушно-сухом состоянии угол естественного откоса песчаного грунта
равен 30-40°, под водой – 24-33°. Для грунтов, не обладающих сцеплением
(сыпучих), угол естественного откоса не превышает угла внутреннего трения
Для определения угла естественного откоса песчаного грунта в воздушно-сухом состоянии используют прибор УВТ (рис. 9.11, 9.12 ), под водой – ВИА (рис. 9.13 ).
Согласно рис. 9.12 при наклоне ящика песок осыпается и, разрыхляясь, образует откос с углом, который можно определить транспортиром или по формуле
Понятие об угле естественного откоса относится только к сухим сыпучим грунтам, а для связных глинистых оно теряет всякий смысл, так как у последних он зависит от влажности, высоты откоса и величины пригрузки на откос и может изменяться от 0 до 90°.
Рис. 9.11. Прибор УВТ-2: 1 – шкала; 2 – резервуар; 3 – мерительный
столик; 4 – обойма; 5 – опора; 6 – образец песка
9.11. Прибор УВТ-2: 1 – шкала; 2 – резервуар; 3 – мерительный
столик; 4 – обойма; 5 – опора; 6 – образец песка
Рис. 9.12. Определение угла естественного откоса вращением емкости (а) и медленным снятием пластинки (б): А – ось вращения емкости
Рис. 9.13. Прибор ВИА: 1 – ящик ВИА; 2 – образец песка; 3 – емкость с водой; 4 – транспортир; 5 – ось вращения; 6- пьезометр; 7- штатив
При разработке и усадке разрыхленного грунта выемки и насыпи образуют естественные откосы различной крутизны. Наибольшую крутизну плоских откосов земляных сооружений, траншей и котлованов, устраиваемых без креплений, следует принимать согласно табл. 9.2. При обеспечении естественной крутизны откосов обеспечивается устойчивость земляных насыпей и выемок.
Таблица 9.2. Наибольшая крутизна откосов траншей и котлованов, град.
| 1,5 | 3,0 | 5,0 | |
| Насыпные неуплотненные | 56(1:0,67) | 45(1:1) | 38(1:1,25) |
| Песчаные и гравийные влажные | 63(1:0,5) | 45(1:1) | 45(1:1) |
| Глинистые: | |||
| супесь | 76(1:0,25) | 56(1:0,67) | 50(1:0,85) |
| суглинок | 90(1:0) | 63(1:0,5) | 53 (1:0,75) |
| глина | 90(1:0) | 76(1:0,25) | 63(1:0,5) |
| Лессы и лессовидные сухие | 90(1:0) | 63(1:0,5) | 63(1:0,6) |
| Моренные: | |||
| песчаные, супесчаные | 76(1:0,25) | 60(1:0,57) | 53 (1:0,75) |
| суглинистые | 78(1:0,2) | 63(1:0,5) | 57(1:0,65) |
Откосы насыпей постоянных сооружений выполняют более пологими, чем откосы
выемок.
Общие положения
Назначение и виды земляных сооружений
Объем земляных работ очень большой, он имеется при строительстве любого здания и сооружения. Из общей трудоемкости в строительстве земляные работы составляют 10%.
Различаются следующие основные виды земляных сооружений :
Планировка площадки;
Котлованы и траншеи;
Земляные полотна дорог;
Плотины;
Каналы и др.
Земляные сооружения делятся на :
Постоянные;
Временные.
К постоянным относятся котлованы, траншеи, насыпи, выемки.
К постоянным земляным сооружениям предъявляются требования :
Должно быть прочным, т.е. сопротивляться временным и постоянным нагрузкам;
Устойчивым;
Хорошо сопротивляться атмосферным влияниям;
Хорошо сопротивляться размывающим действиям;
Должны обладать безосадочностью.
Основные строительные свойства и классификация грунтов
Грунтом называют породы, залегающие в верхних слоях земной коры. К ним относятся: растительный грунт, песок, супесь, гравий, глина, суглинок лессовидный, торф, различные скальные грунты и плывуны.
К ним относятся: растительный грунт, песок, супесь, гравий, глина, суглинок лессовидный, торф, различные скальные грунты и плывуны.
По крупности минеральных частиц и их взаимной связи различают следующие грунты :
Связные – глинистые;
Несвязные – песчаные и сыпучие (в сухом состоянии), крупнообломочные несцементированные грунты содержащие более 50% (по массе) обломков кристаллических пород размером более 2 мм;
Скальные – изверженные, метаморфические и осадочные породы с жесткой связью между зернами.
К основным свойствам грунтов, влияющим на технологию производства, трудоемкость и стоимость земляных работ относятся :
Объемная масса;
Влажность;
Размываемость
Сцепление;
Разрыхленность;
Угол естественного откоса;
Объемной массой называется масса 1 м3 грунта в естественном состоянии в плотном теле.
Объемная масса песчаных и глинистых грунтов 1,5 – 2 т/м3, скальных не разрыхленных до 3 т/м3.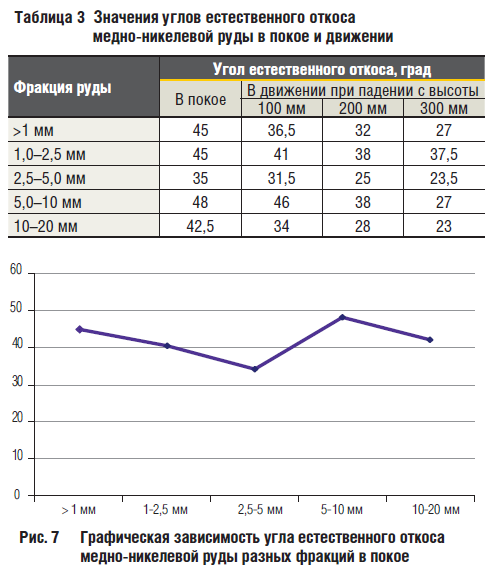
Влажность – степень насыщения пор грунта водой
g b – g c – масса грунта до и после сушки.
При влажности до 5% – грунты называются сухие. При влажности от 5 до 15% – грунты называются маловлажными. При влажности от 15 до 30% – грунты называются влажные.
При влажности более 30% – грунты называются мокрые.
Сцепление – начальное сопротивление грунта сдвигу.
Сила сцепления грунтов : – песчаных грунтов 0,03 – 0,05 МП- глинистых грунтов 0,05 – 0,3 МП- полускальных грунтов 0,3 – 4 МПа- скальных более 4 МПа.
В мерзлых грунтах сила сцепления значительно больше.
Разрыхляемость – это способность грунта увеличиваться в объеме при разработке, вследствие потери связи между частицами. Увеличение объема грунта характеризуется коэффициентом разрыхления К р. После уплотнения разрыхленного грунта называется остаточной разрыхленностью К ор.
Угол естественного откоса характеризуется физическими свойствами грунта. Величина угла естественного откоса зависит от угла внутреннего трения, силы сцепления и давления вышележащих слоев. При отсутствии сил сцепления предельный угол естественного откоса равен углу внутреннего трения. Крутизна откоса зависит от угла естественного откоса. Крутизна откосов выемок и насыпей характеризуется отношением высоты к заложению m – коэффициент откоса.
Величина угла естественного откоса зависит от угла внутреннего трения, силы сцепления и давления вышележащих слоев. При отсутствии сил сцепления предельный угол естественного откоса равен углу внутреннего трения. Крутизна откоса зависит от угла естественного откоса. Крутизна откосов выемок и насыпей характеризуется отношением высоты к заложению m – коэффициент откоса.
Углы естественного откоса грунтов и отношение высоты откоса к заложению
| Грунты | Значение углов естественного откоса и отношений высоты откоса к его заложению при различной влажности грунтов | |||||
| Сухой | Влажный | Мокрый | ||||
| Угол в град | Угол в град | Отношение высоты к заложению | Угол в град | Отношение высоты к заложению | ||
| Глина | 1: 1 | 1: 1,5 | 1: 3,75 | |||
| Суглинок средний | 1: 0,75 | 1: 1,25 | 1: 1,75 | |||
| Суглинок легкий | 1: 1,25 | 1: 1,75 | 1: 2,75 | |||
| Песок мелкозернистый | 1: 2,25 | 1: 1,75 | 1: 2,75 | |||
| Песок среднезернистый | 1: 2 | 1: 1,5 | 1: 2,25 | |||
| Песок крупнозернистый | 1: 1,75 | 1: 1,6 | 1: 2 | |||
| Растительный грунт | 1: 1,25 | 1: 1,5 | 1: 2,25 | |||
| Насыпной грунт | 1: 1,5 | 1: 1 | 1: 2 | |||
| Гравий | 1: 1,25 | 1: 1,25 | 1: 1,5 | |||
| Галька | 1: 1,5 | 1: 1 | 1: 2,25 |
Размываемость грунта – унос частиц текучей водой. Для мелких песков наибольшая скорость воды не должна превышать 0,5-0,6 м/сек, для крупных песков 1-2 м/сек, для глинистых грунтов 1,5 м/сек.
Для мелких песков наибольшая скорость воды не должна превышать 0,5-0,6 м/сек, для крупных песков 1-2 м/сек, для глинистых грунтов 1,5 м/сек.
Угол естественного откоса
предыдущийследующийКогда контейнер, полный гранулированного материала, выливается на плоскую горизонтальную поверхность из точечного источника, такого как воронка, он образует коническую кучу материала. Эта коническая свая будет иметь характерный угол естественного откоса или, что эквивалентно, наклон естественного откоса.Угол естественного откоса – это угол между горизонтальной поверхностью и наклонной поверхностью сваи. Тангенс этого угла и есть крутизна покоя.
Ваш браузер не поддерживает видео тег.
Ваш браузер не поддерживает видео тег.
Экспериментально установлено, что угол естественного откоса определяется рядом факторов.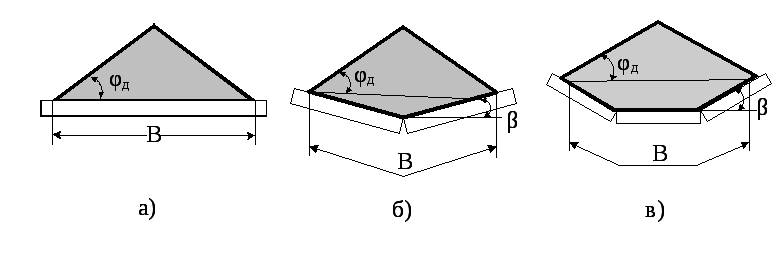 Одним из очевидных факторов является трение, а вторым – когезия, вызванная наличием жидких мостиков между гранулами, которые позволяют гранулам слипаться.
Одним из очевидных факторов является трение, а вторым – когезия, вызванная наличием жидких мостиков между гранулами, которые позволяют гранулам слипаться.
Простые эксперименты со стеклянными бутылками с завинчивающейся крышкой, наполовину заполненными мелкозернистым рыхлым песком, могут показать различные аспекты поведения сыпучего материала. На видео ниже показаны две бутылки с песком: одна наполовину заполнена песком и наполовину наполнена воздухом, а вторая – наполовину наполнена песком и наполовину наполнена водой.
Если для начала обе бутылки медленно перекатить по бокам на горизонтальном столе, песок в обеих бутылках переместится, образуя упаковки гранул с плоскими горизонтальными поверхностями.
Если наполовину заполненную песком и наполовину заполненную воздухом бутылку наклонить, чтобы встать на ее конец, можно увидеть, что песок образует наклон с определенным углом естественного откоса. Если бутылку дополнительно наклонить в том же направлении, будет видно, что совокупность гранул на склоне течет таким образом, что отдельные гранулы вращаются на , когда они текут вниз по склону, а не скользят вниз на склоне в чтобы сохранить угол естественного откоса.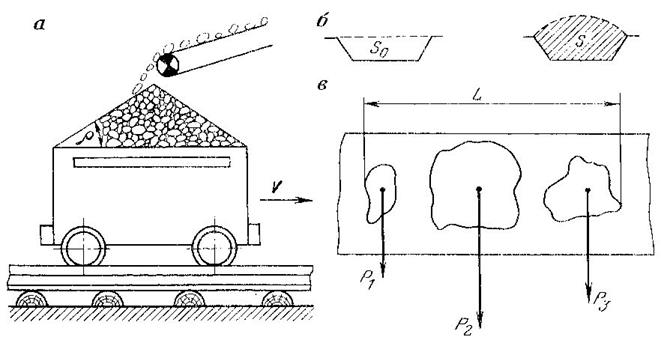
Если бутылку, наполовину заполненную песком и наполовину наполненную водой, наклонить, чтобы она стояла на конце, результат зависит от временной шкалы, в течение которой происходит наклон.
Если масштаб времени короткий, например, менее секунды, поверхность песка разрушается таким образом, что гранулы в конечном итоге уплотняются до горизонтальной поверхности, так что поверхность ведет себя так, как если бы она была жидкостью.
Если наклон происходит постепенно, например, в течение нескольких секунд, можно увидеть, что наклон, достигаемый песком, когда бутылку наклоняют, чтобы встать на ее конец, в пределах экспериментальной ошибки такой же, как и для бутылки, наполовину полной. песка и наполовину заполнен водой.Если еще больше наклонить бутылку, гранулы на склоне будут вести себя так же, как в воздухе.
В глинах, таких как лондонская глина, консолидировавшаяся за 50 миллионов лет (https://en.wikipedia.org/wiki/London_Clay), большие куски сколотых блоков глины, известные как «жирные спинки», могут падать с поверхностей туннелей в течение раскопки.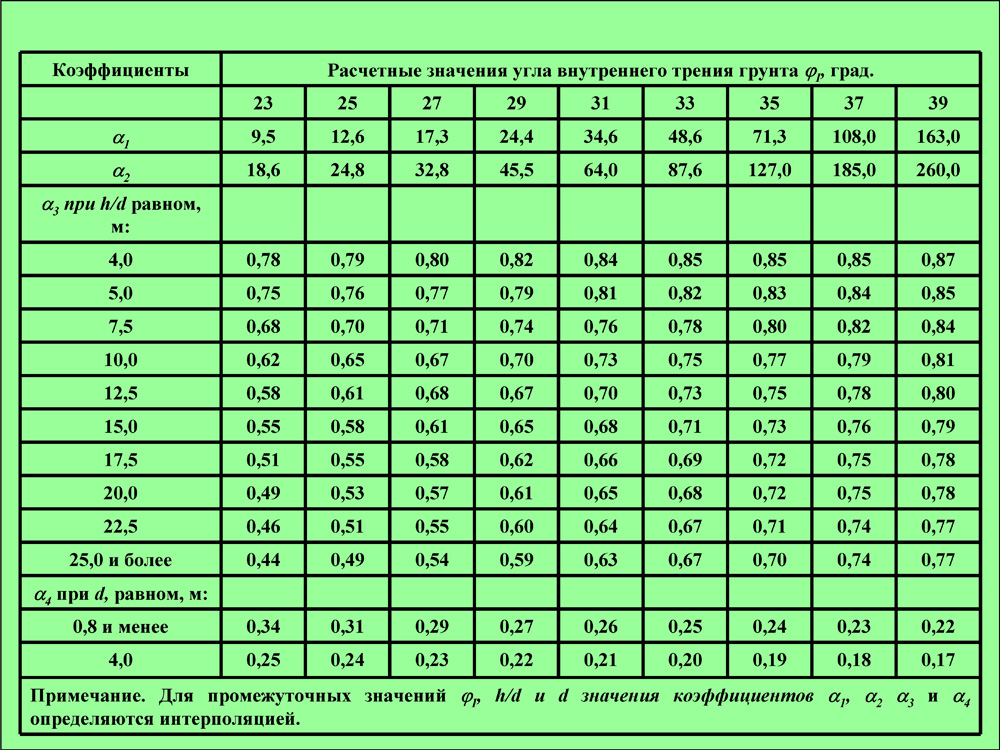 Нижние поверхности этих раздробленных блоков состоят из участков почвы, в которых произошло локальное расширение, и где процесс разрушения при сдвиге является следствием вращения гранул в этих областях, как если бы они падали под углом естественного откоса, а не на поверхность. перевод гранул.Исследование поверхностей этих засаленных задних поверхностей после разрушения показывает, что они имеют характеристики пластифицированной глиняной пасты, напоминающей смазку для тяжелых двигателей (C.N.P. Mackenzie, Traditional Timbering in Soft Ground Tunnel: A Historical Review, British Tunneling Society, 2014).
Нижние поверхности этих раздробленных блоков состоят из участков почвы, в которых произошло локальное расширение, и где процесс разрушения при сдвиге является следствием вращения гранул в этих областях, как если бы они падали под углом естественного откоса, а не на поверхность. перевод гранул.Исследование поверхностей этих засаленных задних поверхностей после разрушения показывает, что они имеют характеристики пластифицированной глиняной пасты, напоминающей смазку для тяжелых двигателей (C.N.P. Mackenzie, Traditional Timbering in Soft Ground Tunnel: A Historical Review, British Tunneling Society, 2014).
Прогнозы угла естественного откоса
Предсказать угол естественного откоса для определенного семейства гранул непросто: большинство углов естественного откоса получают из экспериментальных измерений, таких как те, которые указаны в статье Википедии об «Угол откоса» (https: // en.wikipedia.org/wiki/Angle_of_repose). Для многих сыпучих материалов типичный угол естественного откоса составляет от 25 ° до 40 °.
Для гладких сферических частиц одинакового размера можно использовать очень простую модель, чтобы оценить, как упаковка сфер в трех измерениях влияет на стабильность уклонов. Предположим, что три идентичные сферические частицы на склоне угла θ относительно горизонтальной упаковки вместе так, что они образуют основу правильного тетраэдра, если четвертая идентичная сфера добавлена поверх этих трех частиц.В зависимости от ориентации φ основания тетраэдра относительно наклона тетраэдр будет устойчивым, если угол θ увеличить от нуля (когда частицы находятся на горизонтальном основании) до критического угла θ c , при котором четвертая сфера скатывается вниз по склону от трех идентичных сфер (предполагается, что все они удерживаются (просто) трением на склоне под этим углом).
При определенном угле φ и θ простая геометрия показывает, что верхняя сфера устойчива только в том случае, если вектор, определяющий силу тяжести, направлен через проекцию подходящего базового треугольника на горизонтальную плоскость.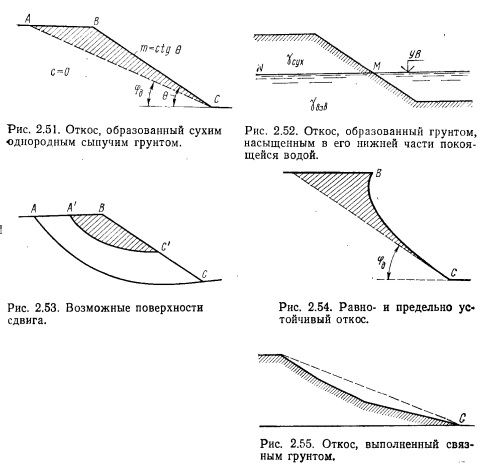 \ circ – \ varphi)}} {\ rm {}} \]
\ circ – \ varphi)}} {\ rm {}} \]
Здесь приводится доказательство этой формулы.
Следовательно, когда φ = 0 °, когда один из углов базового треугольника находится в самой низкой точке на уклоне θ c = 35,26 °, и когда φ = 60 °, когда одна из сторон базового треугольника находится в самой нижней точке склона, θ c = 19,47 °.
График зависимости θ c от φ показан ниже.
Если предположить, что ориентация оснований таких тетраэдров случайна на груде гранулированного вещества, то наблюдаемый угол естественного откоса для гладких несвязных частиц можно утверждать как среднее значение θ c в интервале 0 ° <φ <60 °, т.е.е., 23,8 °, определяется численно с использованием правила Симпсона или правила трапеции. Это соответствует эффективному коэффициенту трения tan θ c , равному 0,44.
Угол естественного откоса
Почему вулканы имеют такую форму? Почему все они имеют коническую форму? *
Гора Фудзи (Изображение: hoge asdf) * Мне достоверно сообщили, что не все вулканы имеют коническую форму. На самом деле такую форму имеют только вулканы шлакового конуса. Щитовые, Купольные и Композитные вулканы имеют разные формы, чтобы отразить различные процессы их образования.
На самом деле такую форму имеют только вулканы шлакового конуса. Щитовые, Купольные и Композитные вулканы имеют разные формы, чтобы отразить различные процессы их образования.
По форме он похож на груды песка, груды зерна и песчаные дюны. Если вы насыпите соль на стол или посмотрите, как текут песочные часы, вы увидите ту же форму. Что происходит?
Это сочетание силы тяжести и трения. Крупинки песка, камня или пепла уносятся вниз под действием силы тяжести; они хотят плыть вниз по склону.Однако они также захватываются другими частицами, уже находящимися на склоне. Этот захват называется трением. Острые, грубые или липкие предметы имеют большее трение и большую силу захвата. Гладкие или скользкие вещества захватываются меньше.
Сила трения пропорциональна нормальной реакции (сила, перпендикулярная направлению, в котором объект пытается двигаться), а предельное отношение этой силы к нормали является безразмерной константой, называемой коэффициентом трения . Обычно это обозначается символом μ
Обычно это обозначается символом μ
Как видно из диаграммы выше, существует зависимость между углом наклона и коэффициентом трения. Когда частица падает на склон, если угол ниже критического, она останется на месте. Если угол больше критического (определяемого арктангенсом коэффициента трения), то он не может захватить и скользит вниз по склону.
Именно такое поведение (примененное осесимметрично) над сваей создает форму конуса, а крутизна конуса пропорциональна коэффициенту трения.
Инженеры называют этот угол Угол естественного откоса . |
Исследование трения и взаимосвязи между поверхностями, движущимися относительно друг друга, называется Трибология . Если вы посмотрите вокруг, вы найдете множество примеров этого явления.
Изображения: Эрни Рейес, jamiesrabbits
Углы естественного откоса
Вот некоторые образцы материалов и их углы естественного откоса.
| Материал | Уголок |
|---|---|
| Ясень | 40 ° |
| Мел | 45 ° |
| Земля | 30 ° -45 ° |
| Сухой гравий | 30 ° -45 ° |
| Сухой песок | 34 ° |
| Мокрый песок | 45 ° |
| Снег | 38 ° |
Большая яма Каркун
Поклонники «Звездных войн» * знают, что те же силы могут быть применены к перевернутой версии формы.Вместо определения конического выступа те же принципы физики могут определять коническое углубление, наклон которого находится под тем же критическим углом.
Может быть, вы испытали это в детстве, когда копали яму на пляже? По мере того, как вы копаете глубже, вы обнаруживаете, что вам нужно увеличивать диаметр отверстия, так как стороны отверстия продолжают разрушаться. |
Есть некоторые умные животные, которые используют этот принцип в своих интересах, чтобы поймать молитву. Один из них – муравейник. Личинка муравьиного льва создает в сухом песке коническое углубление, а на дне прячется. Угол сторон впадины равен углу естественного откоса. Ничего не подозревающее идущее насекомое, такое как муравей, при столкновении с откосом соскользнет на дно ямы; неспособность набрать силу, чтобы вытащить себя, поскольку каждая попытка подняться по склону ослабляет частицы, которые критически сбалансированы и отправляют все скольжение вниз на дно ямы и в ожидающие челюсти муравьиного льва. |
* «Таким образом, вы будете доставлены к Морю Дюны и брошены в Яму Каркуна, место гнездования всемогущего Сарлакка». – Перевод C-3PO слов Джаббы Хатта Хану Соло, Люку Скайуокеру и Чубакке.
– Перевод C-3PO слов Джаббы Хатта Хану Соло, Люку Скайуокеру и Чубакке.
Вы можете найти полный список всех статей здесь. Щелкните здесь, чтобы получать уведомления по электронной почте о новых статьях.
33,4: Угол естественного откоса – Engineering LibreTexts
Когда контейнер, полный гранулированного материала, выливается на плоскую горизонтальную поверхность из точечного источника, такого как воронка, он образует коническую кучу материала.Эта коническая свая будет иметь характерный угол естественного откоса или, что эквивалентно, наклон естественного откоса. Угол естественного откоса – это угол между горизонтальной поверхностью и наклонной поверхностью сваи. Тангенс этого угла и есть крутизна покоя.
Экспериментально установлено, что угол естественного откоса определяется рядом факторов.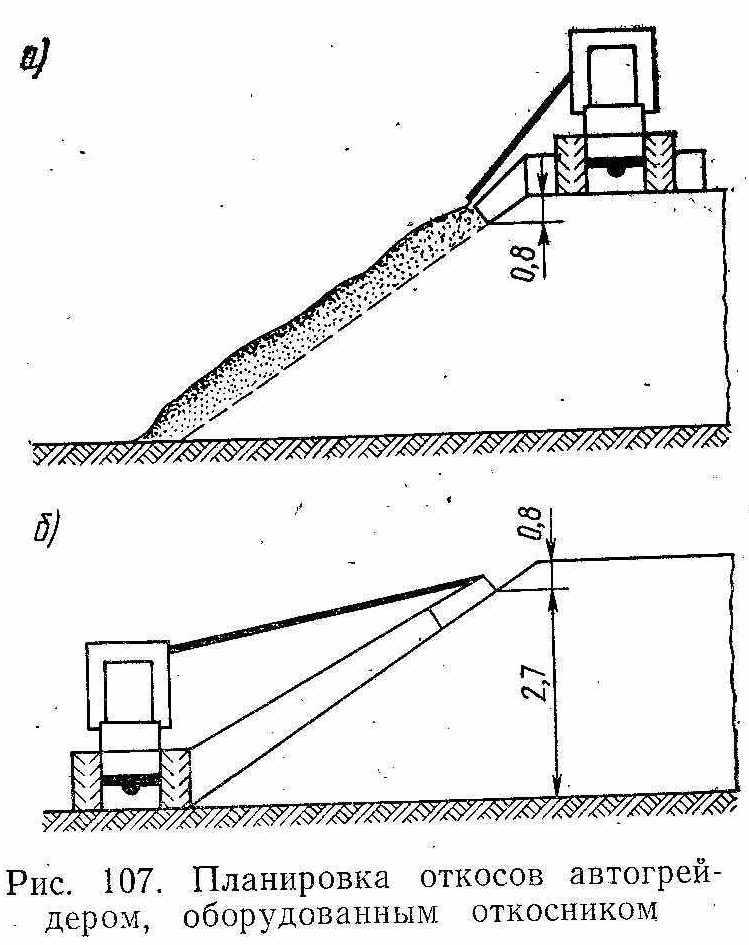 Одним из очевидных факторов является трение, а вторым – когезия, вызванная наличием жидких мостиков между гранулами, которые позволяют гранулам слипаться.
Одним из очевидных факторов является трение, а вторым – когезия, вызванная наличием жидких мостиков между гранулами, которые позволяют гранулам слипаться.
Простые эксперименты со стеклянными бутылками с завинчивающейся крышкой, наполовину заполненными мелкозернистым рыхлым песком, могут показать различные аспекты поведения сыпучего материала. На видео ниже показаны две бутылки с песком: одна наполовину заполнена песком и наполовину наполнена воздухом, а вторая – наполовину наполнена песком и наполовину наполнена водой.
Если для начала обе бутылки медленно перевернуть по бокам на горизонтальном столе, песок в обеих бутылках переместится, образуя упаковки гранул с плоскими горизонтальными поверхностями.
Если наполовину заполненную песком и наполовину заполненную воздухом бутылку наклонить, чтобы встать на ее конец, можно увидеть, что песок образует наклон с определенным углом естественного откоса. Если бутылку дополнительно наклонить в том же направлении, будет видно, что совокупность гранул на склоне течет таким образом, что отдельные гранулы вращаются на , когда они текут вниз по склону, а не скользят вниз на склоне в чтобы сохранить угол естественного откоса.
Если бутылку, наполовину заполненную песком и наполовину наполненную водой, наклонить, чтобы она стояла на конце, результат зависит от временной шкалы, в течение которой происходит наклон.
Если масштаб времени короткий, например, менее секунды, поверхность песка разрушается таким образом, что гранулы в конечном итоге уплотняются до горизонтальной поверхности, так что поверхность ведет себя так, как если бы она была жидкостью.
Если наклон происходит постепенно, например, в течение нескольких секунд, можно увидеть, что наклон, достигаемый песком, когда бутылку наклоняют, чтобы встать на ее конец, в пределах экспериментальной ошибки такой же, как и для бутылки, наполовину полной. песка и наполовину заполнен водой.Если еще больше наклонить бутылку, гранулы на склоне будут вести себя так же, как на воздухе.
В глинах, таких как лондонская глина, консолидировавшаяся за 50 миллионов лет (en.Wikipedia.org/wiki/London_Clay), большие комки обтесанных блоков глины, известные как «жирные спинки», могут падать с поверхностей туннелей во время раскопок. Нижние поверхности этих раздробленных блоков состоят из участков почвы, в которых произошло локальное расширение, и где процесс разрушения при сдвиге является следствием вращения гранул в этих областях, как если бы они падали под углом естественного откоса, а не на поверхность. перевод гранул.Исследование поверхностей этих засаленных задних поверхностей после разрушения показывает, что они имеют характеристики пластифицированной глиняной пасты, напоминающей смазку для тяжелых двигателей (C.N.P. Mackenzie, Traditional Timbering in Soft Ground Tunnel: A Historical Review, British Tunneling Society, 2014).
Прогнозы угла естественного откоса
Предсказать угол естественного откоса для определенного семейства гранул непросто: большинство углов естественного откоса получают из экспериментальных измерений, таких как те, которые цитируются в статье Википедии об «Угол откоса» (en.Wikipedia.org/wiki/Angle_of_repose). Для многих сыпучих материалов типичный угол естественного откоса составляет от 25 ° до 40 °.
Для гладких сферических частиц одинакового размера можно использовать очень простую модель, чтобы оценить, как упаковка сфер в трех измерениях влияет на стабильность уклонов. Предположим, что три идентичные сферические частицы на склоне угла θ относительно горизонтальной упаковки вместе так, что они образуют основу правильного тетраэдра, если четвертая идентичная сфера добавлена поверх этих трех частиц.В зависимости от ориентации φ основания тетраэдра относительно наклона тетраэдр будет устойчивым, если угол θ увеличить от нуля (когда частицы находятся на горизонтальном основании) до критического угла θ c , при котором четвертая сфера скатывается вниз по склону от трех идентичных сфер (предполагается, что все они удерживаются (просто) трением на склоне под этим углом).
При определенном угле φ и θ простая геометрия показывает, что верхняя сфера устойчива только в том случае, если вектор, определяющий силу тяжести, направлен через проекцию подходящего базового треугольника на горизонтальную плоскость.{\ circ} – \ varphi}}) \]
Здесь приводится доказательство этой формулы.
Следовательно, когда φ = 0 °, когда один из углов базового треугольника находится в самой низкой точке на уклоне θ c = 35,26 °, и когда φ = 60 °, когда одна из сторон базового треугольника находится в самой нижней точке склона, θ c = 19,47 °.
График зависимости θ c от φ показан ниже.
Если предположить, что ориентация оснований таких тетраэдров случайна на груде гранулированного вещества, то наблюдаемый угол естественного откоса для гладких несвязных частиц можно утверждать как среднее значение θ c в интервале 0 ° <φ <60 °, т.е.е., 23,8 °, определяется численно с использованием правила Симпсона или правила трапеции. Это соответствует эффективному коэффициенту трения tan θ c , равному 0,44.
Характеристика угла естественного откоса бинарных сыпучих материалов
Если у вас установлено соответствующее программное обеспечение, вы можете загрузить данные цитирования статей в выбранный вами менеджер цитирования. Просто выберите программное обеспечение менеджера из списка ниже и нажмите «Загрузить».
Цитируется по
1. Характеристика бинарных смесей окатышей и агломерата для моделирования методом DEM
2. Влияние сегрегации частиц на неравномерное распределение электростатического заряда в цилиндрическом бункере во время загрузки бинарных частиц с соотношением размеров 2,5: 1 централизованно
3. Анализ системы измерения угла естественного откоса удобрений с разным гранулометрическим составом
4. Экспериментальное исследование распределения вертикального напряжения под зернистыми силосами
5. Моделирование угла естественного откоса сыпучих материалов на основе данных DEM
6. Влияние мелких частиц на реологические свойства порошков диоксида урана
7. Влияние тестовой геометрии и текстуры агрегата на угол естественного откоса агрегатов
8. Моделирование текучести грунта с использованием метода дискретных элементов (DEM)
9. Обзор угла естественного откоса сыпучих материалов
10. Коллапс зернистых колонн с фрактальным распределением частиц по размерам: последствия для понимания роли мелких частиц в зернистых потоках
11. Поведение различных геосинтетических армированных грунтовых структур при сдвиге по результатам испытаний на прямой сдвиг
13. Сравнение методов для измерения угла естественного откоса сыпучих материалов
14. Разработка нового прибора для оценки текучести частиц с плохим поведением потока
15. Микро- и макромасштабные коэффициенты трения вяжущих материалов
16. MAHLI в песчаной тени Rocknest: наука и научная деятельность
17. Моделирование потоков сыпучих материалов: угол естественного откоса, флюидизация и обрыв проблема коллапса
18. Роль угловатости частиц на механическое поведение гранулированных смесей
19. Исследование влияния скорости крыльчатки на гранулы, сформированные с помощью гранулятора с большим сдвигом PMA-1
20.
24. Статические и текучие области в гранулированных обрушениях вниз по каналам: выводы из модели осадконакопления на мелководье
25. Структурная устойчивость бетонных гравитационных плотин, усиленных каменной наброской: гидростатическая нагрузка
Выражение для угла естественного откоса сухих связных гранулированных материалов на Земле и в планетных средах
Угол естественного откоса, спрогнозированный по модели DEM.
На рис. 1 показаны снимки моделирования, полученные с d = 30 мкм и d = 1 мм в условиях земной гравитации. Для измерения угла естественного откоса рассчитывается проекция кучи на две ортогональные плоскости (x и y), что дает два изображения кучи сбоку, разделенных поворотом на 90 °. Затем применяется алгоритм обработки изображений для вычисления верхней границы гранулированного материала, то есть поверхности кучи, а также общей площади поверхности, связанной с двумерной проекцией кучи.Следуя исх. 18, мы определяем угол естественного откоса как угол основания равнобедренного треугольника, который имеет такую же площадь поверхности, как и куча (рис. 1). Таким образом, для каждой кучи получают два значения этого угла, из которых вычисляют среднее значение θr и SD σθr. Мы не обнаружили значительных изменений угла естественного откоса при включении вычислений этого угла из дополнительных выступов, разделенных меньшими углами поворота (18).
Рис. 1.Снимки гранулированных куч, полученные в ходе нашего моделирования.В A мы видим кучу, состоящую из частиц диаметром d = 30 мкм, в то время как размер частиц в B составляет d = 1 мм. Пролет каждой кучи равен 40 дн, и обе кучи были созданы с использованием земной силы тяжести.
Более того, мы обнаружили, что груды, образованные частицами диаметром меньше значения dc (≈50 мкм под действием земной гравитации), имеют сильно неправильную форму со значительными вариациями местного наклона по всей их поверхности (Рис. 1 A ). В этом режиме сильно нерегулярной морфологии кучи, который мы называем здесь режимом I, лавины частиц в значительной степени сдерживаются образованием больших, нерегулярных агломератов частиц вдоль поверхности кучи.Напротив, кучи, образованные с частицами размера d≳dc (режим II), имеют довольно регулярную морфологию и почти постоянный уклон вдоль своей поверхности (рис. 1 B ).
Мы отмечаем, что становится все труднее создавать кучи в нашем моделировании, когда d уменьшается до значений, меньших, чем dc. В частности, мы не смогли получить какую-либо кучу для d менее примерно 50% от постоянного тока, поскольку липкое поведение частиц для таких малых размеров частиц приводит к тому, что куча достигает верхнего предела области моделирования.Таким образом, выводы, представленные в нашей статье, применимы к отвалам в режиме II, т.е. при условии, что размер частиц не превышает примерно dc.
Сплошные квадраты на рис. 2 обозначают значения θr (d), полученные при моделировании DEM под действием силы тяжести Земли. Кроме того, на рис.2 также представлена комплексная подборка экспериментальных данных для угла естественного откоса как функции размера частиц, взятых из измерений θr в гранулированных кучах, изготовленных из различных материалов (см. Легенду и обозначение на рис.2). Как видно на рис. 2, наши численные прогнозы замечательно следуют тенденции экспериментальных данных.
Рис. 2.Зависимость угла естественного откоса от диаметра частиц. Сплошные синие квадраты обозначают прогнозы, полученные в результате численного моделирования, выполненного с параметрами, перечисленными в таблице 1, и с использованием g = 9,81 м / с2. Остальные символы обозначают экспериментальные наблюдения, сделанные для примерно монодисперсных систем, то есть сценарий нашего моделирования DEM. Все приведенные экспериментальные данные соответствуют стеклянным шарикам (1, 2, 5, 19⇓⇓ – 22), за исключением Pilpel (3) (оксид магния) и Lumay et al.(18) (абразивы из карбида кремния). Сплошная линия обозначает наилучшее соответствие нашим численным прогнозам с использованием уравнения. 1 , что дает DE≈87 мкм, а μэфф, ∞≈0,447.
Кроме того, на рис. 3 A показаны значения θr, полученные для различных значений силы тяжести, от силы тяжести Плутона (g = 0,62 м / с2) до силы тяжести, в 100 раз превышающей земную. Мы видим, что одинаковое качественное поведение θr как функции от d наблюдается для всех исследованных значений силы тяжести. Более того, для данного размера частиц наблюдается тенденция увеличения θr с уменьшением силы тяжести.В следующем разделе мы представляем математическое выражение, которое прольет свет на наши численные прогнозы, а также на экспериментальные наблюдения угла естественного откоса как функции размера частиц.
Рис. 3.Влияние силы тяжести на угол естественного откоса. В A символы обозначают θr (d) для различных уровней g, от условий гравитации на Плутоне до 100-кратной силы тяжести Земли. Сплошные линии на этом графике показывают наилучшее соответствие данным моделирования с использованием уравнения. 1 , предполагая μeff, ∞ = 0.447. Кроме того, символы в B обозначают угол естественного откоса θr, nc, полученный при моделировании без сил сцепления, а пунктирная линия в A и B указывает значение θr, ∞≡tan − 1 [μeff, ∞ ]. Значения D, полученные из наилучшего соответствия в A , показаны в C как функция уровня g. Сплошная линия в C представляет уравнение. 2 , используя DE = 87 мкм, полученный на основе наилучшего соответствия данным DEM с учетом силы тяжести Земли (рис.2). Кроме того, пунктирная линия обозначает наилучшее соответствие нашим численным прогнозам D как функции g̃ с использованием D = D0 / g̃α, что дает D0≈76 мкм и α≈0,454 с коэффициентом корреляции более 99%.
Математическое выражение для угла естественного откоса как функции силы тяжести и размера частиц.
Чтобы получить математическое выражение, которое соответствует нашим прогнозам DEM для θr как функции размера частиц, сначала отметим, что угол естественного откоса описывается как θr≈tan − 1 [μeff], где μeff – эффективный коэффициент трения, описывающий максимальное сопротивление трению гранулированного материала лавинному скольжению (23).Этот коэффициент кодирует информацию о свойствах материала, а также о макроскопических характеристиках, связанных со структурой кучи, таких как фракция упаковки и шероховатость поверхности.
Однако на эти характеристики влияет характер сил межчастичного взаимодействия. По мере уменьшения размера частицы силы взаимодействия притягивающих частиц становятся все более значимыми по сравнению с силами гравитации, тем самым приводя к увеличению объемной пористости и влияя на динамику распределения напряжений в куче.Эксперименты и моделирование с помощью DEM показали, что твердая фракция порошков приблизительно подчиняется степенной зависимости от размера частиц (15). Вдохновленные этим пониманием, мы приближенно описываем θr (в радианах), используя выражение θr≈tan − 1μeff, ∞⋅1 + Dd, [1] где эффективный коэффициент трения μeff, ∞ и характерный масштаб D должны определяться из лучше всего подходит для наблюдений за углом естественного откоса как функцией размера частиц. Наилучшее соответствие нашим данным моделирования (синие сплошные квадраты на рис.2) с использованием уравнения. 1 дает μeff, ∞≈0,447 и D≈87 мкм, с коэффициентом корреляции R2≈99%. Это наилучшее соответствие обозначено сплошной линией на рис. 2.
Более того, сплошные линии на рис. 3 A обозначают наилучшее соответствие результатам DEM, связанным с различными значениями уровня г ; т.е. g̃ = g / gEarth, где gEarth = 9,81 м / с2, используя уравнение 1 и предполагая, что μeff, ∞≈0,447 не зависит от силы тяжести. Пунктирная линия на рис. 3 A соответствует асимптотическому значению угла естественного откоса, θr, ∞≡tan − 1 [μeff, ∞].Действительно, мы находим, что угол естественного откоса θr, nc, полученный при моделировании без сил взаимодействия притягивающих частиц (т. Е. В предположении несвязных материалов), приблизительно равен θr, ∞, независимо от размера частиц (рис. 3 B ). Наблюдается небольшая тенденция увеличения θr, nc под действием силы тяжести – рис. 3 B предполагает увеличение порядка 10% в θr, nc с увеличением g̃ от 0,06 до 100, что мы приписываем несколько большей тенденции частиц к сцеплению при увеличении гравитационного напряжения, но дальнейшая работа ( не входит в объем данной статьи), чтобы прояснить этот небольшой эффект.Рис. 3 A и B , таким образом, показывает, что контроль размера частиц на θr в основном продиктован связными взаимодействиями частица-частица.
Рис. 3 C отображает значения D, полученные из наилучшего соответствия на рис. 3 A , как функцию уровня g. Как видно из рис. 3 C , для диапазона g̃, рассматриваемого в настоящей работе, характерный масштаб D можно приближенно описать уравнением D = DEg̃, [2] где DE обозначает земное значение D , я.е., 87 мкм. Отметим, что сплошная красная линия на рис. 3 C не соответствует данным моделирования (сплошные кружки). Вместо этого красная линия обозначает уравнение. 2 , т.е. наша гипотеза о том, что D равно DE / g̃. Мы обнаружили, что аппроксимация результатов DEM с использованием уравнения D = D0 / g̃α приводит к D0≈76 мкм и α≈0,45 с коэффициентом корреляции более 99% (пунктирная линия на рис. 3 C ), что дает, таким образом, , показатель степени близок к 0,5, как предполагается в уравнении. 2 .
Используя уравнение. 2 мы можем переписать уравнение. 1 asθr≈tan − 1μeff, ∞⋅1 + 1 (d / DE) ⋅g̃, [3] который предоставляет средства для оценки θr (в радианах) для заданных g и d, при условии, что DE и μeff, ∞ для гранулированный материал известен, например, из экспериментов при земной гравитации.
Из уравнения. 3 , мы видим, что в пределе g̃d / DE → ∞ угол естественного откоса асимптотически приближается к значению θr, ∞≡tan − 1 [μeff, ∞], независимо от силы тяжести и размера частиц. Для исследуемого порошкового материала θr, ∞≈24 ° (рис.2 и 3). Следовательно, приблизительное значение μeff, ∞ можно оценить из экспериментов с использованием частиц, которые настолько велики, что когезионными эффектами на угол естественного откоса можно пренебречь, после чего μeff, ∞ можно вычислить с помощью уравнения μeff, ∞ = tan (θr, ∞). Впоследствии эксперименты под действием силы тяжести Земли с использованием различных значений d могут быть выполнены для оценки DE от наилучшего соответствия уравнению. 3 .
Чтобы пролить свет на Ур. 3 , отметим, что зернистые материалы демонстрируют возрастающую относительную когезию, чем меньше размер частиц (15).Мы следим за исх. 24 и 25, и охарактеризуйте эту когезию, вычислив число Бонда (Bo), то есть отношение максимальной силы сцепления, действующей на частицу, к силе гравитации. Для системы, исследуемой здесь, мы получаем Bo = 12γ / (d2gρp) (используя уравнения 13 и 14 ), где ρp – плотность материала, а γ – поверхностная плотность энергии, которая масштабирует притягивающую межчастицу ( Ван-дер-Ваальс) сила. Учитывая это выражение для числа Бонда и масштабирование угла естественного откоса с размером частиц в формуле. 3 , мы предлагаем модель θr≈tan − 1μeff, ∞⋅1 + βBo, [4] где μeff, ∞ и β – эмпирические параметры. Как показано на рис. 4, используя эту модель, мы обнаружили превосходный коллапс данных наших результатов моделирования для всех рассмотренных значений размера частиц и силы тяжести с μeff, ∞≈0,458 и β≈0,014. Кроме того, из определения Bo, уравнения. 1 и 4 приводят к D = β12γρpg, [5] что связывает характерный масштаб длины D в уравнении. 1 к параметрам материала.
Фиг.4.Основной график: угол естественного откоса θr как функция числа Бонда. Символы указывают на прогнозы численного моделирования при различных уровнях g . Более того, сплошная линия на основном графике обозначает наилучшее соответствие данным моделирования с использованием уравнения. 4 , что дает μeff, ∞≈0,458 и β≈0,014 (R2≈0,98). Данные, показанные на основном графике, перенесены на вставку , которая показывает угол естественного откоса θr как функцию от Bo с использованием линейной шкалы для обеих осей.
Отметим, что наша модель работает в режиме регулярной морфологии кучи (режим II), т.е.е., когда d≳dc. В частности, уравнение. 1 предсказывает θr → 90 °, когда d → 0, но эксперименты показали почти постоянный угол естественного откоса для частиц размером порядка нескольких микрометров, то есть в режиме I нерегулярной морфологии кучи (26). Наше моделирование показывает, что D≈2dc и что морфология кучи изменяется с регулярной (режим II) на нерегулярную (режим I), когда число Бонда превышает примерно 104, что позволяет приблизительно оценить постоянный ток по свойствам материала.
Мы также выполнили моделирование с кучей на 150% больше, чем рассматриваемые в настоящем обсуждении, но мы не смогли найти значительного изменения в значениях θr.Мы считаем, что качественно даже большие кучи должны демонстрировать такую же зависимость θr от d, наблюдаемую в экспериментах, приведенных на рис. 2, и в моделировании DEM в этой статье. Однако неясно, в какой степени параметры нашей модели должны быть адаптированы для количественной оценки угла естественного откоса гораздо больших отвалов. В частности, на динамику гораздо более крупных систем могут влиять взаимодействия частицы с воздухом, которые должны быть включены в будущее расширение нашей модели. Кроме того, поскольку на динамику упаковки влияет история приготовления упаковки (см. Обсуждение в исх.15), высота заливки и размер области введения, выбранные для воспроизведения экспериментальных условий, могут оказывать важное влияние на значение θr. Мы действительно заметили тенденцию к увеличению размеров лавины за счет увеличения ширины области вставки частиц в нашем моделировании больших куч. Следовательно, количественное поведение θr для гораздо больших куч станет темой будущих исследований.
Аргумент для приблизительного масштабирования с квадратным корнем из числа Бонда в уравнении.
4 .Наша модель предполагает, что эффективный коэффициент трения μeff может быть записан как μeff≈μeff, ∞⋅1 + f, [6] где μeff, ∞ – значение μeff без учета вклада сил взаимодействия притягивающих частиц, закодированного в f. Кроме того, приблизительное масштабирование f с помощью Bo получается из нашего моделирования (уравнение 4 ).
Чтобы пролить свет на это масштабирование, отметим, что, когда местный уклон превышает угол естественного откоса, поверхность отвала расслабляется за счет лавины, что приводит к появлению поверхностного лавинообразного слоя толщиной в несколько раз, состоящего из N частиц – стекающие вниз по неподвижной гранулированной массе внутри кучи.Под углом естественного откоса нисходящая гравитационная сила, действующая на эти N частиц, то есть W = Nmg, где m обозначает массу частицы, уравновешивается контактными силами трения и когезионными взаимодействиями с частицами в объеме. Однако не все N частиц участвуют в этих взаимодействиях. Вместо этого общая сила сцепления действует на подмножество поверхностей частиц, которые находятся на границе раздела с основной массой. Мы предполагаем, что f масштабируется как отношение этой общей силы сцепления к W; т.е. f∝Ninterface⋅FvdWNmg∝NinterfaceN⋅1d2g, [7] где мы использовали m∝d3 и FvdW∝d, где FvdW обозначает притягивающую силу Ван-дер-Ваальса (уравнение. 13 ) между частицей в лавинообразном слое и другой частицей в объеме. Следовательно, масштабирование f с помощью Bo, т.е. с dg − 1, получается, если η≡Ninterface / N∝dg, что необходимо проверить с помощью численного моделирования.
Однако здесь мы предполагаем, что η в первом порядке пропорционален плотности упаковки (ϕ) гранулированного материала. Мы считаем это предположение разумным, поскольку чем меньше ϕ, тем пористее зернистая среда и, следовательно, меньше η. Напротив, чем плотнее гранулированный материал, тем больше число контактов между частицами и, таким образом, больше η.Чтобы проверить, следует ли ϕ (и, следовательно, η), до определенного предела, приблизительному масштабированию с dg, мы провели численные эксперименты, адаптируя протокол исх. 15 для исследования влияния d и g на ϕ. На рис. 5 показаны результаты этих экспериментов, которые описаны в конце документа «Материалы и методы» .
Рис. 5.Плотность упаковки ϕ как функция dg̃, с g̃≡g / gEarth. Пунктирная линия на основном графике обозначает наилучшее соответствие результатам моделирования (символы) с использованием уравнения ϕ = ϕ∞⋅1 − C⋅exp − Dϕ − 1⋅dg̃, которое дает ϕ∞≈0.57, C≈0,56 и Dϕ≈103 мкм, при R2≈0,994. Кроме того, сплошная линия на вставке обозначает наилучшее линейное соответствие результатам моделирования в диапазоне 30≤d / мкм≤210, используя ϕ = A + B⋅dg̃, что дает A≈0,32 и B≈1,14 мм − 1. , с R2≈0,947.
Как видно на рис. 5, график зависимости ϕ от dg̃ приводит к превосходному коллапсу данных наших результатов моделирования и показывает асимптотический рост доли упаковки с dg̃. В частности, в пределе больших размеров частиц (d≳1 мм) гранулированный материал демонстрирует в значительной степени несвязное поведение, при этом ϕ практически не зависит от dg̃.Пунктирная линия на основном графике на рис. 5 обозначает наилучшее соответствие с использованием асимптотической функции роста ϕ = ϕ∞⋅1 − C⋅exp − Dϕ − 1⋅dg̃, что дает ϕ∞≈0,57 (соответствующая доля случайной неплотной упаковки ) (27), C≈0,56, Dϕ≈103 мкм, с коэффициентом корреляции R2≈0,994. Отметим, что теоретическая модель необходима для объяснения этого масштабирования, а также поведения ϕ при dg̃ → 0. Однако такая теоретическая модель выходит за рамки настоящего обсуждения, которое скорее направлено на проверку приближенного масштабирования ϕ с dg̃ до определенного предела.
Действительно, линейная аппроксимация с использованием ϕ = A + B⋅dg̃ достаточно хорошо описывает тенденцию результатов моделирования, связанных с нижним диапазоном dg̃, рассмотренным в настоящей статье; т.е. 30≤dg̃ / мкм≤210, с A≈0,32, B≈1,14 мм − 1 и коэффициентом корреляции R2≈0,947 (рис. 5, , вставка ). Источником этой приблизительной линейной тенденции является эффект сил взаимодействия притягивающих частиц, которые актуальны в вышеупомянутом диапазоне малых dg̃, но становятся пренебрежимо малыми по сравнению с массой частицы, когда dg̃ становится достаточно большим.Таким образом, мы находим, что приближенное линейное масштабирование ϕ (и, таким образом, η≡Ninterface / N) с dg̃, в диапазоне малых dg̃, дает аргумент в пользу приближенного масштабирования f с Bo, благодаря уравнению. 7 . Точнее, f∝η / d2g∝ϕ / d2g∝1 / dg (т.е. f∝Bo).
Значение нашей модели в свете экспериментальных наблюдений.
Эксперименты с уменьшенной гравитацией образования гранулированной кучи (28) в Бременской башне с использованием базальтовых шариков диаметром 500 мкм выявили небольшую тенденцию увеличения угла естественного откоса с уменьшением силы тяжести для 0.03≤g̃≤1. Хотя эксперименты проводились с использованием ячейки Хеле – Шоу для получения квазидвумерных куч (28), качественно поведение θr с гравитацией для этих куч согласуется с предсказанием нашей модели о том, что зернистые материалы ведут себя более связно и образуют большие углы. покоя при более низкой гравитации.
Кроме того, параболические летные эксперименты с медленно вращающимися барабанами, работающими в режиме дискретной лавины на уровнях g от 0,1 до 1, выявили небольшую тенденцию к увеличению угла естественного откоса θstart – наклона, выше которого зернистая поверхность становится нестабильной и начинает скатываться. лавина (29) – с уменьшением силы тяжести (30, 31).Увеличение θstart с уменьшением g, наблюдаемое в исх. 30 предполагает улучшенное когезионное поведение гранулированных материалов при пониженной гравитации (30). Эксперименты в условиях микрогравитации с вращающимися барабанами, работающими при уровнях g от 0,01 до 1,9 и при высоких скоростях вращения, в так называемом непрерывном лавинообразном режиме, в котором гранулированная поверхность постоянно подвергается лавинообразному потоку, также показали возрастающее когезионное поведение с уменьшением g (32, 33). В этих экспериментах было обнаружено масштабирование угла наклона гранулированной поверхности на 1 / g (32, 33).Для сравнения, эксперименты на центрифуге при уровнях g от 1 до 25 выявили незначительную корреляцию между этим углом и силой тяжести (34), что также было предсказано нашей моделью.
Отметим, что на силы взаимодействия частиц могут влиять все еще плохо изученные геохимические процессы (35), в то время как потоки гранул в условиях низкого атмосферного давления могут подвергаться дополнительному влиянию присутствия порового газа. Более того, для значений числа Бонда, меньших единицы, неправильная геометрия частиц, присущая естественным гранулированным системам, может вызывать статистические флуктуации, сравнимые с разницей между углами естественного откоса, предсказанными для сферических частиц при g-уровнях того же порядка.Например, параболические летные эксперименты с использованием песка Тоёра (d ≈ 250 мкм) не выявили существенной зависимости угла естественного откоса от силы тяжести для диапазона исследованных уровней g (от 1/6 до 2) (36). На основании наших результатов мы заключаем, что угол естественного откоса естественного песка под действием марсианской гравитации не должен сильно отличаться от его земного аналога (от 30 ° до 35 °), что согласуется с наблюдениями на склоне марсианских дюн на их лавинообразной стороне ( 37).
Характеристика среднего размера частиц сильно полидисперсных систем может быть проведена с использованием различных параметров, таких как средний размер частиц по Заутеру dS, т.е.е. диаметр частицы, имеющей такое же отношение объема к площади поверхности, как и весь ансамбль. Две всеобъемлющие компиляции экспериментальных наборов данных по θr как функции dS, представленные в справочниках. 26 и 38, демонстрируют те же характеристики, что и на рис. 2, т.е. заметное степенное уменьшение с dS в промежуточном диапазоне размеров частиц с последующим более медленным распадом в пределе большего dS, при этом θr асимптотически приближается значение θr, ∞ между 20 ° и 30 °, которое примерно не зависит от размера частиц.Таким образом, мы предлагаем, чтобы уравнение. 1 должно быть действительным безотносительно параметра, используемого для характеристики размера частиц, так как соответствующее значение D может быть оценено из наилучшего соответствия θr (d) с использованием уравнения. 1 .
Далее отметим, что уравнение. 1 должен выйти из строя, когда d станет намного меньше определенного значения (dc), которое для системы, рассматриваемой в нашем моделировании DEM, составляет порядка 50 мкм. Действительно, уравнение. 1 предсказывает, что θr → 90 ° при d → 0.Однако измерения θr сильно полидисперсных пылевых систем (с использованием среднего диаметра Заутера dS для характеристики размера частиц) выявили нарушение тенденции увеличения θr с уменьшением размера частиц, когда частицы становятся достаточно мелкими (26). Как пояснил Ланцерсторфер (26), причиной такого поведения является образование небольших агломератов пылевидных частиц, которые скатываются вниз по склону отвала, тем самым ограничивая угол естественного откоса. Верхний предел для θr около 55 ° был сообщен в экспериментах в [5].26.
Хотя потребуется дальнейшая работа для характеристики динамики агломератов частиц в моделировании DEM и для исследования факторов, контролирующих значение dc, мы отмечаем, что самые высокие значения θr в большинстве наборов экспериментальных данных, приведенных на рис. 2, являются согласованными. с верхней границей, полученной Ланцерсторфер (26). Единственное исключение – набор данных Lumay et al. (18) (белые квадраты на рис. 2), где θr превышает 70 °. Возможное объяснение более высоких значений θr в этом наборе данных заключается в том, что абразивы из карбида кремния, принятые в справочнике.18 состоят из широкого спектра частиц сложной геометрической формы, включая удлиненные частицы и частицы с острыми краями. Моделирование методом DEM (39) показало, что когезионные стержни образуют упаковки с более низкой твердой фракцией, чем у связных шариков; т.е. частицы сложной формы могут улучшить когезионные свойства гранулированных материалов. На основании этих наблюдений и с учетом наших формул. 4 и 7 , таким образом, мы ожидаем, что удлиненные частицы, по сравнению с шариками, образуют более крутые кучи, в то время как острые края могут дополнительно улучшить трение и устойчивость кучи.Таким образом, настоящая работа может быть продолжена путем выяснения этого поведения при моделировании DEM.
Однако будущая работа теперь должна быть сосредоточена на углублении понимания наших результатов теоретического анализа стабильности гранулированной кучи, который представляет собой давнюю и сложную исследовательскую тему в области физики гранулированной материи (40).
Скользкие склоны и угол естественного откоса
Основные концепции
Физика
Гравитация
Сил
Угол естественного откоса
Введение
Вы когда-нибудь видели видеозапись схода лавины или оползня с холма? Почему в какой-то момент все кажется прекрасным, а потом гора внезапно начинает падать? Это движение имеет какое-то отношение к тому, как на горе накапливается снег или почва.Гранулированные материалы, такие как снег или почва, обычно относительно хорошо накапливаются. Однако если угол наклона станет слишком большим, материалы начнут соскальзывать вниз по склону. Этот критический угол наклона, также называемый углом естественного откоса, различен для разных материалов. В этом упражнении вы будете создавать свои собственные небольшие лавины и определять угол естественного откоса для различных материалов по пути!
Фон
Если на ровную поверхность насыпать сыпучий материал, он образует конусообразную стопку.Если добавить больше материала, ворс вырастет. Однако в какой-то момент угол наклона сваи всегда останется неизменным. Это связано с тем, что по мере того, как свая растет и ее наклон достигает определенного угла, часть материала соскальзывает вниз по свае. Это угол естественного откоса и самый крутой угол, при котором материал может складываться в кучу без соскальзывания вниз. Но почему материал скользил?
Причина в гравитации. Сила тяжести, действующая на материал на склоне, может быть разделена на два разных компонента: первая, нормальная сила, втягивает материал в склон в направлении, перпендикулярном поверхности склона.Нормальная сила тянет внутрь зерна на склоне, что на самом деле помогает удерживать зерна вместе и предотвращает скольжение материала вниз. В зависимости от типа и формы материала силы трения между зернами также могут удерживать их вместе. В результате зерна неправильной формы, которые могут сцепляться, как правило, имеют больший угол естественного откоса. Вторая гравитационная составляющая – это поперечная сила, которая тянет зерна вниз по склону в направлении, параллельном поверхности склона.Чем круче наклон, тем выше будет сила сдвига. В какой-то момент поперечная сила преодолеет нормальную силу тяжести. Обычно это момент, когда материалы начинают скользить по склону и достигается угол естественного откоса.
Это может показаться очень теоретической концепцией. Однако существует множество ситуаций, когда зерна, такие как кукуруза, мука или гравий, необходимо складывать в кучу. В этих ситуациях знание их угла естественного откоса может быть очень полезным для определения правильных размеров силоса для хранения или для разработки конвейерной ленты нужного размера для их транспортировки.Угол естественного откоса также используется для оценки возможности обрушения горного склона. Это помогает геологам или альпинистам заранее узнать о рисках схода лавин! Есть несколько способов измерить угол естественного откоса конкретного материала. Один из них, которым вы будете заниматься в этом упражнении, включает в себя измерение высоты и радиуса сваи, образованной материалом, а затем использование этих чисел для вычисления угла естественного откоса.
Материалы
- Помощник для взрослых
- Ножницы
- Одноразовая пластиковая чашка, 16 унций
- Бумага для принтера
- Форма для выпечки
- Ручка
- Линейка
- Рулетка
- Соль поваренная (минимум одна чашка)
- Рис (минимум одна чашка)
- Сахарная пудра (минимум одна чашка)
- Научный калькулятор или приложение с функциями научного калькулятора
- Дополнительные гранулированные материалы, такие как чечевица, мука и т. Д.
- Транспортир (опция)
Подготовка
- С помощью взрослого вырежьте небольшое отверстие в нижней части пластикового стаканчика.Его диаметр должен быть около двух сантиметров.
Процедура
- Поместите лист бумаги для принтера в форму для выпечки и промаркируйте его материалом, который вы хотите протестировать.
- Прикрыв отверстие чашки рукой или пальцами, заполните чашку первым материалом как минимум наполовину.
- Держите чашку вплотную к верхней части бумаги принтера в центре. Затем уберите руку или пальцы, чтобы высвободить материал внутри чашки. Что вы замечаете, когда материал падает на бумагу?
- По мере роста груды материала держите чашку выше, чтобы весь материал упал на бумагу. В зависимости от материала вам может потребоваться немного постучать по чашке, чтобы она все вышла. Обратите внимание на угол наклона сваи по мере ее роста. Угол наклона меняется со временем? Как выглядят ворс материала и угол наклона в конце?
- Ручкой аккуратно проведите по окружности ворса материала.Будьте осторожны, чтобы не повредить ворс слишком сильно. Насколько большой или маленький ваш круг?
- С помощью линейки измерьте высоту (h) ворса материала в сантиметрах. Вы можете очень осторожно вставить линейку в стопку, чтобы измерить ее высоту на вершине. Если этот метод слишком сильно мешает ворсу, вы также можете подержать линейку рядом с ворсом и осторожно протянуть рулетку от верха ворса до линейки. Высота стопки – это место пересечения рулетки и линейки.Запишите высоту стопки на листе бумаги рядом с ней. Какова высота вашей стопки материала?
- Используя нарисованный круг и измеренную высоту, вычислите угол естественного откоса для этого материала. Уравнение для расчета угла естественного откоса: tan -1 (h / r). Не волнуйтесь, если уравнение выглядит сложным – вы определите каждое число шаг за шагом, а остальное сделает калькулятор!
- Удалите материал с листа бумаги.Используя линейку, измерьте два разных диаметра (d) нарисованного круга в сантиметрах. Для этого проведите две линии от одного случайного края круга через его центр к противоположному краю. Длина каждой линии даст вам диаметр круга. Запишите оба числа. Цифры сильно различаются? Что это говорит вам о форме круга?
- Рассчитайте средний диаметр вашего круга, сложив оба измеренных диаметра и разделив результат на два.Исходя из этого, вы можете рассчитать радиус (r) вашего круга, снова разделив средний диаметр на два.
- Используйте калькулятор, чтобы разделить измеренную высоту (в сантиметрах) на рассчитанный радиус (в сантиметрах). Запишите результат с точностью до одной десятичной точки.
- Теперь осталось только ввести это число в калькулятор и нажать клавишу арктангенса (или tan-1). Это даст вам угол естественного откоса. Запишите это на листе бумаги.
- Повторите эти шаги со всеми другими материалами. Чем отличаются форма и размер каждой кучи материала? Какой материал имеет самый низкий или самый высокий угол естественного откоса? Вы ожидали таких результатов?
- Экстра: Протестируйте еще несколько материалов. Подойдет любой сыпучий материал. Другие возможности для тестирования: песок, кофейные зерна, гравий, кукурузный крахмал и т. Д. Как эти материалы соотносятся с протестированными вами?
- Extra: Используйте транспортир, чтобы измерить угол естественного откоса непосредственно от стопки, которую вы создали с каждым материалом. Насколько хорошо ваш измеренный угол совпадает с рассчитанным углом естественного откоса?
Наблюдения и результаты
Как выглядели ваши стопки? Каждый из ваших материалов должен образовывать красивый конический ворс. Окружность каждой сваи должна быть близка к симметричной окружности, что означает, что два измеренных диаметра должны быть относительно одинаковыми. Однако высота свай и размеры измеренных кругов должны были измениться в зависимости от материалов, которые вы тестировали.Рис, вероятно, образовывал большие круги, тогда как сахарная пудра, вероятно, образовывала очень маленькие круги. И наоборот, высота кучи риса должна быть значительно ниже, чем у сахарной пудры.
Основываясь на этих числах, вы, вероятно, обнаружили, что рис имеет небольшой угол естественного откоса (от 25 до 30 градусов), тогда как сахарная пудра имеет относительно большой угол (более 40 градусов). Расчетный угол соли должен быть где-то посередине. Это изменение связано с разными размерами и формой частиц материала.Увеличение размера частиц обычно уменьшает угол естественного откоса. Вот почему большие частицы риса имеют гораздо меньший угол, чем у мелкозернистой сахарной пудры. Кроме того, частицы неправильной формы держатся вместе намного лучше, чем очень круглые частицы, которые легко перекатываются друг по другу.
Очистка
Если вы использовали чистые материалы, вы можете повторно использовать рис, соль и сахарную пудру. Очистите рабочее место и вымойте руки.
Дополнительные сведения для изучения
Факторы, влияющие на устойчивость откосов, из Физическая геология
Оползни: что заставляет скалы спускаться со склона? Оползень и другие гравитационные движения, из Разъясненных наукой
Занятия STEM для детей, из Ученых друзей
Эта деятельность предоставлена вам в сотрудничестве с Science Buddies
(PDF) Сравнение между углом естественного откоса и углом трения песка
12
-я
Международная конференция
Международная ассоциация компьютерных методов и достижений в геомеханике (IACMAG)
1-6 октября, 2008
Гоа, Индия
Сравнение между углом естественного откоса и углом трения
Песок
M.Газави
Кафедра гражданского строительства, Технологический университет К. Н. Туси, Тегеран, Иран
М. Хоссейни
Кафедра гражданского строительства, Технологический университет К. Н. Туси, Тегеран, Иран
М. Молланури
Кафедра Гражданское строительство, Технологический университет К. Н. Туси, Тегеран, Иран
Ключевые слова: лабораторный эксперимент, песок, угол естественного откоса, угол трения, испытание на прямой сдвиг.
РЕФЕРАТ: Можно сказать, что форма отложения песка обычно коническая, и песчинки ориентированы под определенным углом
отложения и естественного отложения.Этот угол таков, что не возникает стабильности. Таким образом, угол естественного откоса составляет
, что несколько коррелирует с углом внутреннего трения песка. В данной статье представлены результаты серии
лабораторных экспериментов сэкспериментами, выполненными на трех типах песка. Для этого подготовлено специальное приспособление. Устройство
хорошо оборудовано и позволяет насыпать песок с разной высоты. После заливки песка с определенной высоты,
угол естественного откоса измеряется с использованием геометрии отложения песка.Испытания на прямой сдвиг также проводятся на песке
при таком же уплотнении для определения угла трения. Затем эти два угла соотносятся. Результаты
показывают, что угол естественного откоса можно коррелировать с внутренним трением песка. Эмпирическое выражение
представлено для корреляции этих двух, позволяя пользователям оценить угол трения песка в поле
.
1 Введение
Обычно видно, что когда отвал грунта насыпается на участок, он имеет форму конуса.Угол между конусом почвы
и горизонтальным направлением, очевидно, зависит от параметров почвы, таких как угол внутреннего трения
, гранулометрический состав, форма зерна, удельный вес, содержание влаги, расслоение, сегрегация и т. Д. На угол также влияет метод и процедура заливки, включая высоту заливки грунта, а также статическую или динамическую заливку
. Фактически, угол естественного откоса является одним из наиболее важных макроскопических параметров в
, характеризующих поведение сыпучих материалов, и поэтому в течение многих лет находится в центре внимания исследований.Было обнаружено
, что угол естественного откоса сильно зависит от свойств материала, таких как трение скольжения и качения (Lee and
,Herrmann, 1993; Hill and Kakalios, 1995; Zhou et al., 1999)
и плотности частиц (Burkalow, 1945) и
характеристик частиц, таких как размер [8,13] и форма (Burkalow, 1945; Carrigy, 1970), в дополнение к методу
формирования песчаной кучи для формирования песчаной кучи (Grasselli and Herrmann , 1997; Kalman, et al., 1993). Обычно сообщается, что угол естественного откоса
увеличивается с увеличением коэффициентов трения скольжения и качения и отклонения
от сфер и уменьшается с увеличением размера частиц.
В этой статье был сделан прибор для определения ангела покоя из-за засыпания песчаной почвы с
различных высот. Параллельно с этим были проведены испытания на прямой сдвиг для определения угла внутреннего трения песка
. Затем эти углы сравниваются, и результаты будут представлены.
2 Описание испытательного устройства
Специальное устройство было изготовлено из металла, как показано на рисунке 1. Это устройство состоит из четырех стержней с резьбой
, расположенных вокруг, чтобы сделать резервуар размером 70
70 см в плане. Плоская стальная металлическая пластина использовалась в качестве дна контейнера
для создания горизонтальной поверхности. Некоторые стержни использовались для основных элементов рамы. Несколько стальных стержней
также использовались в качестве ремней вокруг рамы для устойчивости вертикальных стержней.Горизонтальные и вертикальные стержни
были сварены вместе. Вертикальные стержни имели резьбу, чтобы облегчить изменение высоты засыпки песка в резервуар.
Для подачи песка в резервуар использовалось отдельное хранилище.

 ОБЩИЕ ПОЛОЖЕНИЯ .. 1
ОБЩИЕ ПОЛОЖЕНИЯ .. 1 9
9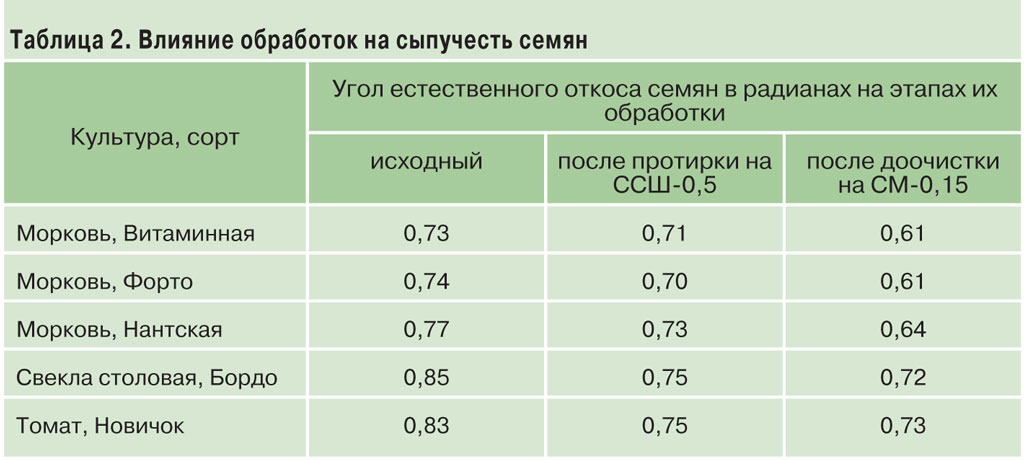 Производство лабораторных исследований физико-механических
свойств грунтов.
Производство лабораторных исследований физико-механических
свойств грунтов. № 42
№ 42 Существует критический угол (который, как мы теперь знаем, равен , угол покоя ), после которого стенки больше не могут поддерживать частицы, и они скользят внутрь.Мокрый песок имеет более высокий коэффициент трения, чем сухой песок, поэтому во влажном можно вырыть ямы с более крутыми сторонами.
Существует критический угол (который, как мы теперь знаем, равен , угол покоя ), после которого стенки больше не могут поддерживать частицы, и они скользят внутрь.Мокрый песок имеет более высокий коэффициент трения, чем сухой песок, поэтому во влажном можно вырыть ямы с более крутыми сторонами.
Добавить комментарий