Крутизна откоса что такое: Крутизна откосов — ТехЛиб СПБ УВТ
Крутизна откосов — ТехЛиб СПБ УВТ
Из Пособия по проектированию земляного полотна и водоотвода железных и автомобильных дорог промышленных предприятий (к СНиП 2.05.07-85).
2.20. Крутизну откосов насыпей и выемок следует назначать в зависимости от вида грунта, высоты насыпи и глубины выемки с учетом инженерно-геологических, гидрологических и мерзлотных условий, а также способа производства работ и метода укрепления откосов согласно СНиП 2.05.07-85, п. 2.56.
2.21. Откосы насыпей, выемок и других грунтовых сооружений, подверженных разрушению под воздействием природных, техногенных и антропогенных факторов, должны быть укреплены. Тип укрепления следует назначать в зависимости от конструкции сооружения, интенсивности воздействия природных факторов и физико-механических свойств грунтов.
На подтопляемых откосах в укреплении следует предусматривать обратный фильтр из дренирующих грунтов или геотекстиля. Отметка верха укрепления подтопляемых откосов должна быть выше отметки наибольшего уровня воды, определяемого с учетом наката волны подпора воды на откос.
2.22. При сложных инженерно-геологических и гидрогеологических условиях крутизну откосов назначают:
в выемках глубиной более 12 м: в скальных слабовыветривающихся грунтах, при применении скважинных зарядов методом контурного взрывания допускается устройство вертикальных откосов;
В выемках глубиной до 6 м: в глинистых пылеватых грунтах в районах с избыточным увлажнением следует принимать 1 : 2, глубиной более 6 м — устанавливают расчетом;
в выемках, сооружаемых в легковыветривающихся скальных грунтах и в лессах, следует проектировать с учетом опыта строительства и эксплуатации земляного полотна в рассматриваемом районе;
в выемках в легковыветривающихся неразмягчаемых скальных грунтах — от 1 : 0,5 до 1 : 1,5;
в выемках глубиной до 2 м — 1 : 3 и более;
в выемках, сооружаемых в районах подвижных песков на участках с полузаросшей и заросшей растительностью, крутизну откосов разрешается принимать равной углу естественного откоса песка, но не более 1 : 1,5.
2.23. При проектировании откосов выемок на бортах карьеров высоту устойчивого откоса и его крутизну рекомендуется назначать по табл. 6.
Таблица 6
Скальные грунты в откосах карьеров | Средний размер блоков породы в массиве, м | Высота откоса борта карьера, м | Рекомендуемая крутизна откоса |
| Монолитные | Более 1,5 | 20 и более | 1 : 0,1 |
| Крупноблочные (малотрещиноватые) | 1,5 — 1 | До 20 | 1 : 0,1 — 1 : 0,2 |
| Крупноблочные (среднетрещиноватые) | 1 — 0,5 | До 16 | 1 : 0,2 |
| Среднеблочные (трещиноватые) | 0,5 — 0,1 | До 12 | 1 : 0,2 — 1 : 0,5 |
| Мелкоблочные (сильнотрещиноватые) | Менее 0,1 | До 6 | 1 : 0,5 — 1 : 1 |
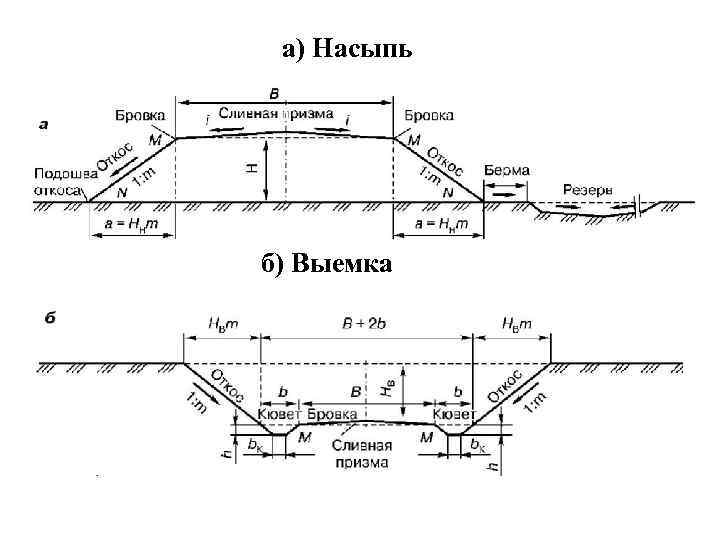
2. 24. Откосы насыпей, сооружаемых из дренирующих грунтов над поверхностью болота, следует проектировать с уклоном 1 : 1,5, а из мелких и пылеватых песков — в верхней части насыпей с уклоном — 1 : 1,75, а также нижней, считая от поверхности болота на высоту 1 м, — 1 : 3.
24. Откосы насыпей, сооружаемых из дренирующих грунтов над поверхностью болота, следует проектировать с уклоном 1 : 1,5, а из мелких и пылеватых песков — в верхней части насыпей с уклоном — 1 : 1,75, а также нижней, считая от поверхности болота на высоту 1 м, — 1 : 3.
2.25. Крутизна откосов насыпей, возводимых из песчаных грунтов, назначается с учетом вида грунта согласно табл. 7.
Таблица 7
Грунт | Крутизна откосов |
| Пески среднезернистые (на всю высоту насыпи) | 1 : 1,5 |
| Пески мелкие, однородные и пылеватые (для отсыпки верхней части насыпи, выше капиллярного поднятия) на сухих основаниях | 1 : 1,75 |
| Пески среднезернистые (для отсыпки нижней части насыпей на высоту капиллярного поднятия) на сырых и мокрых основаниях, представленных малопросадочными грунтами | 1 : 2 |
| Пески мелкие, пылеватые (для отсыпки нижней части насыпи) на сырых и мокрых основаниях, представленных сильнопросадочными грунтами | 1 : 3 |
2. 26. Крутизну откосов кюветов следует назначать с полевой стороны равной крутизне откосов выемки, а со стороны пути — 1 : 1,5.
26. Крутизну откосов кюветов следует назначать с полевой стороны равной крутизне откосов выемки, а со стороны пути — 1 : 1,5.
Глубину кюветов следует принимать не менее 0,6 м, а ширину по дну — назначать 0,4 м. Для районов с сухим климатом допускается уменьшать глубину кюветов до 0,4 м.
В выемках при расположении путей на уклонах менее 2 ‰ в глубину кюветов в водораздельных (переломных) точках допускается уменьшать до 0,2 м.
В выемках, проектируемых в слабовыветривающихся скальных породах, вместо кюветов допускается устраивать бордюры из камня или бетонных блоков.
Кюветы в легковыветривающихся скальных грунтах допускается проектировать глубиной менее 0,4 м.
В скальных выемках для отвода воды можно использовать кювет-траншеи.
2.27. Размеры поперечного сечения кюветов, нагорных водоотводных канав следует определять расчетом с учетом расхода воды: с вероятностью превышения обеспечения 1 % на линиях категории IВ и 3 % на линиях категории IIВ.
Расчет выполняют по программе автоматизированного гидравлического расчета кюветов и канав (прил. 9).
2.28. Верх земляного полотна, присыпаемого для укладки второго пути, следует проектировать: при недренирующих грунтах с поперечным уклоном в сторону от существующего пути 0,04 в выемках и 0,02 в насыпях. С целью экономии балласта верхнюю часть примыкаемого земляного полотна (выше бровки существующего пути) следует отсыпать из дренирующего грунта.
2.29. Верх земляного полотна железнодорожных путей с заглубленным и полузаглубленным балластным слоем, а также земляного полотна, сооружаемого для укладки нескольких путей (более двух), проектируется односкатным или двускатным. При большем числе путей следует проектировать пилообразный поперечный профиль с устройством в пониженных местах водоотводных лотков.
2.30. Количество путей, располагаемых на одном скате, принимают в зависимости от вида грунта земляного полотна, материала балласта и условий увлажнения на основе технико-экономических расчетов, учитывающих затраты на балластировку и устройство водоотводных сооружений (лотков, дренажей).
Наибольшее число путей на одном скате в зависимости от вида грунта, материала балласта и условий увлажнения, а также величины уклонов скатов определяют по табл. 8.
Таблица 8
Грунты | Материалы балластного слоя | Степень увлажнения | Наибольшее число путей на одном скате | Уклон ската, ‰ |
| Дренирующие | Гравий, пески крупные и средние | Малая | 10 и более | 0 |
| То же, и ракушка | Большая, средняя | 10 | 0 | |
| Недренирующие | Гравий | Малая | 10 — 8 | 1 |
| То же, и ракушка | Большая, средняя | 8 — 6 | 2 | |
| Пески мелкие | Малая | 8 — 6 | ||
| То же, и ракушка | Большая, средняя | 3 — 2 | 2 |
2. 31. Ширину насыпей, сооружаемых на вечномерзлых грунтах, назначают с учетом уширения ее за счет компенсации осадки грунтов основания и тела насыпи в результате оттаивания льдистых грунтов в эксплуатационный период — при подъеме пути на балласт.
31. Ширину насыпей, сооружаемых на вечномерзлых грунтах, назначают с учетом уширения ее за счет компенсации осадки грунтов основания и тела насыпи в результате оттаивания льдистых грунтов в эксплуатационный период — при подъеме пути на балласт.
Уширение основной площадки DВ определяют по формуле
DВ = 2m (Sн + Sо), (1)
где m — крутизна откоса балластной призмы, равная 1,5; Sн — осадка тела насыпи; sо — осадка основания насыпи.
При отсыпке насыпей талых и сыпучемерзлых грунтов при
Н £ 2, Sн = 0, Sэ = (3 — Н) , (2)
2 £ H £ 3, Sн = (H — 2) , Sо = (3 — H) , (3)
где ρстр, ρест — плотность грунтов тела насыпи и естественного основания в строительный период; ρэн, ρэо — плотность грунтов тела насыпи и естественного основания в эксплуатационный период.
Крутизна откосов котлована и траншей
При возведении фундамента под частный дом большое значение имеет крутизна откосов котлована и траншей.
Устройство котлована
При выборе способа выполнения земляных работ учитывают:
- тип конструкции;
- глубину заложения;
- объем работ.
При сооружении ленточного и столбчатого мелкозаглубленного фундамента грунты могут разрабатываться вручную. При строительстве дома с подвалом или цокольным этажом работы должны быть механизированы.
Выемку основного объема грунта выполняет экскаватор с прямой или обратной лопатой. При этом котлован необходимо отрывать без нарушения плотности грунта в основании фундамента. Чтобы соблюсти данное требование, предусматривают недобор грунта в пределах 5-20 см. Зачистку откосов и выемку грунта с основания до проектной отметки выполняют вручную разнорабочие.
Выбираемый грунт должен сразу же вывозиться или размещаться на строительной площадке на расстоянии более 1 м от края котлована.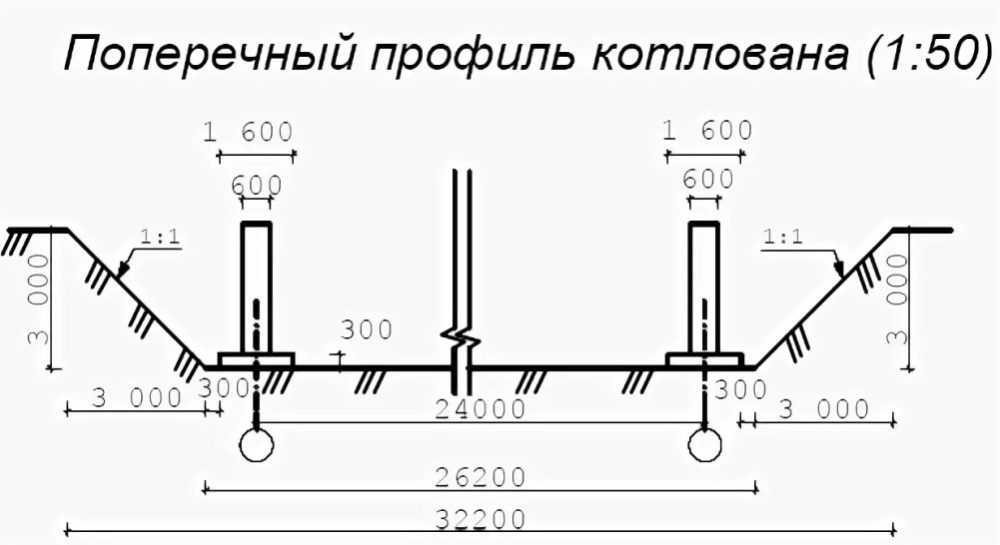
Выбор техники зависит от типа грунта, глубины котлована и объема работ. При строительстве частного дома шириной не более 15 м, можно задействовать экскаватор с обратной лопатой с объемом ковша до 1,4 м3 на колесном или гусеничном шасси.
Значение проектирования откосов
Любой грунт, ограниченный откосами, под действием силы тяжести стремится сдвинуться в сторону откоса, что может привести к неконтролируемому обрушению стенок котлована. Из-за обрушения грунтовых масс могут пострадать рабочие, находящиеся на дне котлована. К тому же это приведет к увеличению объема работ и несоблюдению календарного графика. Так как нужно будет восстанавливать проектный контур котлована, и выполнять обратную засыпку фундамента в большем объеме.
Чтобы избежать травм и не нести убытки, необходимо еще на этапе проектирования рассчитать крутизну откосов котлована и траншей, в соответствии со СНиП 111-4-80.
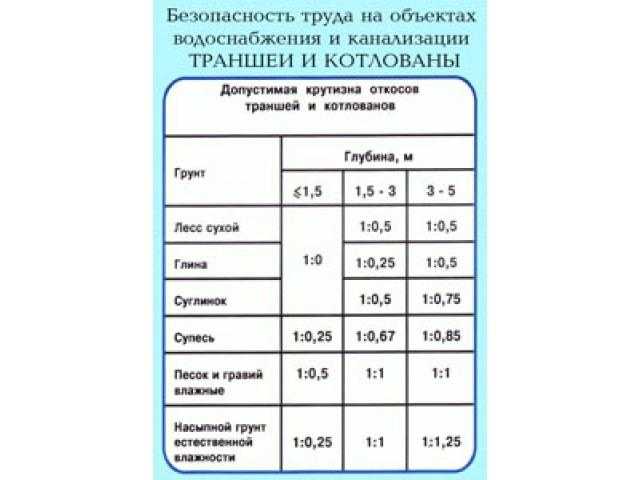
Нормативные данные для проектирования откосов
Устройство котлована с вертикальными без крепления стенками допускается, только при разработке:
- насыпных, песчаных или гравелистых грунтов на глубину не более 1м;
- супесчаных и суглинистых – не более чем на 1,25м;
- глинистых – на 1,5 м;
- особо плотных – на 2 м.

Если же требуется устройство котлована большей глубины, необходимо принять крутизну откосов, рекомендуемую СНиП с учетом типа грунта и глубины заложения. При этом если глубина котлована или траншеи превышает 5 м, то для определения устойчивости земляных масс выполняют расчет.
Крепление стенок котлована глубиной 2-3 м должно выполняться строго по типовому проекту.
В нормативной литературе крутизна откосов котлована и траншей измеряется как угол откоса (ɑ) или отношение высоты откоса к заложению (1:m). В СНиП эти данные приводятся в табличной форме отдельно для каждого типа грунта с учетом глубины выемки.
Если на участке присутствует несколько видов грунта, то крутизну откосов принимают, ориентируясь на самые неустойчивые слои.
В связи с тем, что даже при разработке котлована с откосами не исключена вероятность обрушения грунта под тяжестью машин, необходимо соблюдать требуемое в СНиП расстояние от подошвы откоса до места стояния техники.
Рассчитывая объем земляных работ, учитывают величину откосов, которые увеличивают ширину котлована на b=m*h.
Наклон – определение, типы, примеры
Наклон линии – это мера крутизны и направления линии. Нахождение наклона линий на координатной плоскости может помочь предсказать, параллельны ли линии, перпендикулярны или нет, без фактического использования компаса.
Наклон любой линии можно рассчитать, используя любые две различные точки, лежащие на линии. Формула наклона линии вычисляет отношение «вертикального изменения» к «горизонтальному изменению» между двумя различными точками на линии. В этой статье мы разберемся с методом нахождения уклона и его применениями.
| 1. | Что такое уклон? |
| 2. | Наклон линии |
| 3. | Наклон линии Формула |
| 4. | Как найти уклон? |
5. | Типы уклонов |
| 6. | Наклон перпендикулярных линий |
| 7. | Наклон параллельных линий |
| 8. | Часто задаваемые вопросы о склоне |
Что такое уклон?
Наклон линии определяется как изменение координаты y по отношению к изменению координаты x этой линии . Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как
м = Δy/Δx
где м — уклон
Обратите внимание, что тангенс θ = Δy/Δx
Мы также называем этот тангенс θ наклоном линии.
Наклон линии
Наклон линии представляет собой отношение подъема к пробегу или подъема, деленное на пробег. Он описывает крутизну линии в координатной плоскости. Вычисление наклона линии аналогично нахождению наклона между двумя разными точками. В общем, чтобы найти наклон линии, нам нужно иметь значения любых двух разных координат на линии.
В общем, чтобы найти наклон линии, нам нужно иметь значения любых двух разных координат на линии.
Наклон между двумя точками
Наклон линии можно рассчитать, используя две точки, лежащие на прямой. Зная координаты двух точек, мы можем применить формулу наклона линии. Пусть координаты этих двух точек будут
.
Р 1 = (х 1 , у 1 )
P 2 = (x 2 , y 2 )
Как мы обсуждали в предыдущих разделах, наклон представляет собой «изменение координаты y по отношению к изменению координаты x этой линии». Итак, подставляя значения Δy и Δx в уравнение наклона, мы знаем, что:
Δу = у 2 – у 1
Δx = x 2 – x 1
Следовательно, используя эти значения в соотношении, мы получаем: – x 1 )
где m — наклон, а θ — угол, образуемый линией с положительной осью x.
Формула наклона линии
Наклон линии можно рассчитать по уравнению линии. Общий наклон формулы линии задается как
Общий наклон формулы линии задается как
y = mx + b
где
- м — уклон, такой, что m = tan θ = Δy/Δx
- θ — угол, образуемый линией с положительной осью x
- Δy — чистое изменение по оси Y
- Δx — чистое изменение по оси x
Наклон линии Пример
Вспомним определение наклона линии и попробуем решить приведенный ниже пример.
Пример: Уравнение линии с наклоном 1, проходящей через точку (-1, -5) ?
Решение:
Мы знаем, что если уклон равен 1, то значение м будет равно 1 в общем уравнении y = mx + b. Итак, подставляем значение м в 1, и получаем
y = x + b
Теперь у нас уже есть значение одной точки на прямой. Итак, подставляем значение точки (-1, -5) в уравнение y = x + b, и получаем,
b = -4
Отсюда, подставляя значения m и b в общем уравнении, мы получаем наше окончательное уравнение как y = x – 4.
Уравнение: y = x – 4
Как найти уклон?
Наклон линии можно найти разными способами. Первый метод определения значения уклона заключается в использовании уравнения, которое задается следующим образом: где m – наклон линии.
Кроме того, изменение x равно запустить и изменить y рост или падение . Таким образом, мы также можем определить наклон как m = подъем/спуск
Нахождение наклона на графике
Один из методов нахождения наклона линии на графике заключается в непосредственном применении формулы с учетом координат двух лежащих точек. на линии. Допустим, значения координат двух точек не заданы. Итак, у нас есть еще один способ найти наклон линии. В этом методе мы пытаемся найти тангенс угла, образованного линией с осью x. Следовательно, мы находим наклон, как указано ниже.
Наклон линии имеет только одно значение. Таким образом, наклоны, найденные методами 1 и 2, будут равны.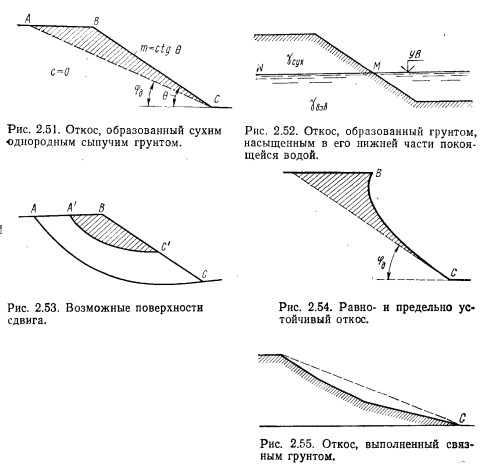 В дополнение к этому, скажем, нам дано уравнение прямой линии. Общее уравнение линии может быть дано как
В дополнение к этому, скажем, нам дано уравнение прямой линии. Общее уравнение линии может быть дано как
y = mx + b
Значение уклона дано как м; , следовательно, значение м дает наклон любой прямой.
Следующие шаги можно выполнить, чтобы найти наклон прямой, такой, что координаты двух точек, лежащих на прямой, равны: (2, 4), (1, 2)
- Шаг 1: Запишите координаты двух точек, лежащих на прямой, (x 2 , y 2 ), (x 1 , y 1 ). Здесь координаты даны как (2, 4), (1, 2).
- Шаг 2: Примените формулу наклона линии, m = (y 2 – y 1 )/(x 2 – x 1 ) = (4 – 2)/(2 – 1) = 2,
- Шаг 3: Следовательно, наклон данной линии = 2.
Типы уклонов
Мы можем классифицировать наклон по различным типам в зависимости от отношения между двумя переменными x и y и, таким образом, от значения градиента или наклона полученной линии. Существует 4 различных типа уклонов, обозначенных как
Существует 4 различных типа уклонов, обозначенных как
- Положительный уклон
- Отрицательный наклон
- Нулевой наклон
- Неопределенный уклон
Положительный наклон
Графически положительный наклон указывает на то, что при движении слева направо в координатной плоскости линия поднимается, что также означает, что при увеличении x увеличивается и y.
Отрицательный наклон
Графически отрицательный наклон указывает на то, что при движении слева направо в координатной плоскости линия падает, что также означает, что при увеличении x уменьшается y.
Нулевой наклон
Для линии с нулевым наклоном подъем равен нулю, и, таким образом, применяя формулу превышения подъема, мы получаем нулевой наклон линии.
Неопределенный уклон
Для линии с неопределенным уклоном значение длины равно нулю. Наклон вертикальной линии не определен.
Наклон горизонтальной линии
Мы знаем, что горизонтальная линия — это прямая линия, параллельная оси x или проведенная слева направо или справа налево в координатной плоскости. Следовательно, чистое изменение координаты y горизонтальной линии равно нулю. Наклон горизонтальной линии можно определить как
Следовательно, чистое изменение координаты y горизонтальной линии равно нулю. Наклон горизонтальной линии можно определить как
Наклон горизонтальной линии, m = Δy/Δx = ноль
Наклон вертикальной линии
Мы знаем, что вертикальная линия — это прямая линия, параллельная оси Y или рисуется сверху вниз или снизу вверх в координатной плоскости. Следовательно, чистое изменение координат x вертикальной линии равно нулю. Наклон вертикальной линии можно определить как
Наклон вертикальной линии, м = Δy/Δx = не определено
Наклон перпендикулярных линий
Набор перпендикулярных линий всегда имеет между собой угол 90º. Предположим, что у нас есть две перпендикулярные линии l 1 и l 2 в координатной плоскости, наклоненные под углами θ 1 и θ 2 соответственно с осью x, так что данные углы следуют внешнему углу теорема как, θ 2 = θ 1 + 90º.
Следовательно, их наклоны можно представить как
м 1 = тангенс θ 1
м 2 = загар (θ 1 + 90º) = – раскладушка θ 1
⇒ m 1 × m 2 = -1
Таким образом, произведение наклонов двух перпендикулярных прямых равно -1.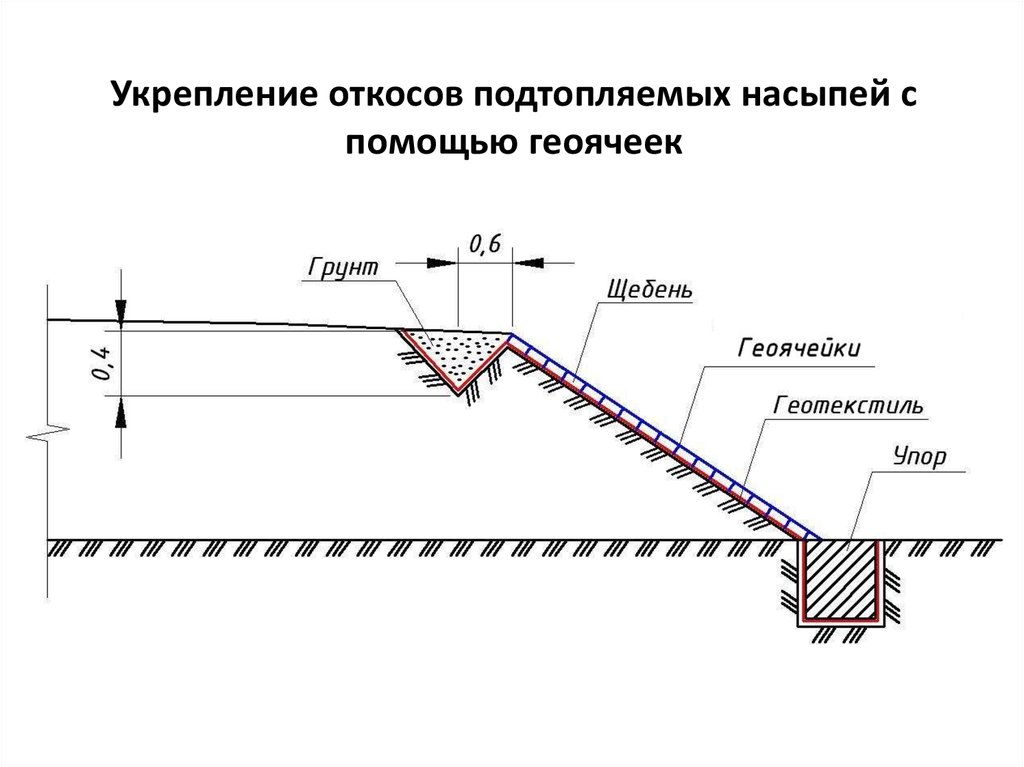
Наклон параллельных линий
Набор параллельных линий всегда имеет одинаковый угол наклона. Предположим, у нас есть две параллельные линии l 1 и l 2 в координатной плоскости, наклоненные под углом θ 1 и θ 2 соответственно с осью x, так что θ 2 = θ 1 .
Следовательно, их наклоны могут быть указаны как
⇒ m 1 = m 2
Таким образом, наклоны двух параллельных прямых равны.
Важные примечания по наклону:
- Наклон линии — это мера тангенса угла, образуемого линией с осью x.
- Наклон постоянен на протяжении всей прямой.
- Форма пересечения наклона прямой линии может быть задана как y = mx + b
- Наклон обозначается буквой m и определяется выражением m = tan θ = (y 2 – y 1 )/(x 2 – x 1 )
Сложный вопрос:
Прямая имеет уравнение y = 2x – 7. Найдите уравнение прямой, перпендикулярной данной прямой и проходящей через начало координат.
Найдите уравнение прямой, перпендикулярной данной прямой и проходящей через начало координат.
☛ Похожие темы:
- Линейное уравнение
- Квадратное уравнение
- Кубическое уравнение
Часто задаваемые вопросы о склоне
Что такое наклон линии?
Наклон линии, также известный как градиент, определяется как значение крутизны или направление линии в координатной плоскости. Уклон можно вычислить разными способами, зная уравнение прямой или координаты точек, лежащих на прямой.
По какой формуле можно найти наклон линии?
Мы можем рассчитать наклон линии напрямую, используя формулу наклона линии, зная координаты двух точек, лежащих на линии. Формула дается как,
Уклон = m = tan θ = (y 2 – y 1 )/(x 2 – x 1 )
Как рассчитать уклон?
Наклон определяется путем измерения тангенса угла, образованного линией с осью x. Существуют различные методы определения наклона линии. Выражение, которое можно использовать для определения наклона, имеет вид tan θ или (y 2 – y 1 )/(x 2 – x 1 ), где θ – угол, который линия образует с положительной осью x, и (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух точек, лежащих на прямой.
Существуют различные методы определения наклона линии. Выражение, которое можно использовать для определения наклона, имеет вид tan θ или (y 2 – y 1 )/(x 2 – x 1 ), где θ – угол, который линия образует с положительной осью x, и (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух точек, лежащих на прямой.
Какие существуют 4 типа склонов?
Существует 4 различных типа наклона: положительный наклон, отрицательный наклон, нулевой наклон и неопределенный наклон.
Что такое неопределенный уклон?
Любой уклон с углом 90º с осью x, будет иметь неопределенное значение тангенса 90º. Следовательно, такие линии будут иметь неопределенное значение наклона.
Как выглядит склон?
Наклон — это не что иное, как мера тангенса угла, составленного с осью x. Следовательно, это всего лишь мера угла.
Какие 3 способа найти уклон?
Способы определения уклона: форма точечного уклона, форма пересечения уклона и стандартная форма. Мы можем применить любую из форм уравнения прямой линии, учитывая необходимую информацию, чтобы найти наклон.
Мы можем применить любую из форм уравнения прямой линии, учитывая необходимую информацию, чтобы найти наклон.
Как показать, что три точки лежат на одной прямой по наклону?
Чтобы доказать коллинеарность трех точек, скажем, A, B и C, мы можем применить формулу наклона. Наклон прямых AB и BC должен быть одинаковым, чтобы три заданные точки были точками на одной прямой.
Как найти уклон по двум точкам?
Наклон можно рассчитать, используя координаты двух точек по формуле m = (y 2 – y 1 )/(x 2 – x 1 ), где (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух точек, лежащих на прямой.
Наклон линии – определение, формулы и примеры
В геометрии мы видели линии, проведенные на координатной плоскости. Чтобы предсказать, являются ли линии параллельными или перпендикулярными, или под любым углом, без использования какого-либо геометрического инструмента, лучший способ определить это — измерить наклон. В этой статье мы подробно обсудим, что такое наклон, формулу наклона для параллельных линий, перпендикулярных линий, уклон для коллинеарности со многими решенными примерами.
В этой статье мы подробно обсудим, что такое наклон, формулу наклона для параллельных линий, перпендикулярных линий, уклон для коллинеарности со многими решенными примерами.
Что такое уклон?
В математике наклоном линии называется изменение координаты y по отношению к изменению координаты x.
Чистое изменение координаты y представлено Δy, а чистое изменение координаты x представлено Δx.
Следовательно, изменение координаты y по отношению к изменению координаты x определяется выражением,
m = изменение y/изменение x = Δy/Δx
Где «м» — наклон линии.
Наклон линии также может быть представлен цифрой 9.0003
тангенс θ = Δy/Δx
Итак, тангенс θ – наклон линии.
Обычно наклон линии определяет ее крутизну и направление. Наклон прямой между двумя точками (x 1 , y 1 ) и (x 2 , y 2 ) можно легко определить, найдя разницу между координатами точек. Уклон обычно обозначается буквой «м».
Уклон обычно обозначается буквой «м».
Формула уклона
Если P(x 1 ,y 1 ) и Q(x 2 ,y 2 ) являются двумя точками на прямой линии, тогда формула наклона определяется как:
| Уклон, м = изменение координаты y/изменение координаты x м = (у 2 – у 1 )/(х 2 – х 1 ) |
Таким образом, на основе приведенной выше формулы мы можем легко вычислить наклон линии между двумя точками.
Другими словами, наклон линии между двумя точками также называется подъемом линии от одной точки к другой (по оси Y) по ходу (по оси X). Следовательно,
Уклон, м = Подъем/Прогон
Уравнение наклона прямой
Уравнение для наклона линии и точек, также называемых точечным наклоном, форма уравнения прямой линии определяется как:
| у – у 1 = м(х – х 1 ) |
Принимая во внимание, что наклон-пересечение формы уравнения линии определяется как:
у = мх + б
Где b — точка пересечения с осью y.
Как найти наклон линии на графике?
На данном рисунке, если угол наклона данной линии с осью x равен θ, то наклон линии определяется тангенсом θ. Следовательно, существует связь между линиями и углами. В этой статье вы узнаете различные формулы, связанные с углами и линиями.
Наклон линии задается как m = tan θ. Если две точки A (x 1 , y 1) и B(x 2 , y 2 ) лежат на прямой с x 1 ≠ x 2 тогда наклон линии AB определяется как:
\(\begin{array}{l} m = tan\ \theta =\frac{y_2~-~y_1}{x_2~-~x_1}\end{массив} \)
Где θ — угол, который линия AB образует с положительным направлением оси x. θ лежит между 0° и 180°.
Следует отметить, что θ = 90° возможно только тогда, когда линия параллельна оси Y, т.е. при x 1 = x 2 при этом конкретном угле наклон линии не определен.
Условия перпендикулярности, параллельности и коллинеарности прямых приведены ниже:
Уклон для параллельных линий
Рассмотрим две параллельные прямые, заданные l 1 и l 2 с наклоном α и β соответственно. Чтобы две прямые были параллельны, их наклон также должен быть равен, т.е. α=β. Это приводит к тому, что тангенс α = тангенс β. Следовательно, условие параллельности двух прямых с наклонами α, β: tan α = tan β.
Чтобы две прямые были параллельны, их наклон также должен быть равен, т.е. α=β. Это приводит к тому, что тангенс α = тангенс β. Следовательно, условие параллельности двух прямых с наклонами α, β: tan α = tan β.
Следовательно, если наклоны двух прямых на декартовой плоскости равны, то эти прямые параллельны друг другу.
Таким образом, если две прямые параллельны, то m 1 = m 2 .
Обобщая это для n линий, они параллельны только тогда, когда наклоны всех линий равны.
Если уравнение двух прямых задано как ax + by + c = 0 и a’ x + b’ y + c’= 0, то они параллельны, когда ab’ = a’b. (Как? Вы можете прийти к этому результату, если найдете наклоны каждой прямой и приравняете их.)
Уклон для перпендикулярных линий
На рисунке две строки l 1 и l 2 с наклоном α, β. Если они перпендикулярны, мы можем сказать, что β = α + 90°. (Используя свойства углов)
Их наклоны могут быть указаны как:
м 1 = тангенс (α + 90°) и м 2 = тангенс α.
\(\begin{array}{l}\Rightarrow m_1 = – кроватка\ \alpha = -~ \frac{1}{tan~\alpha} = -~\frac {1}{m_2}\end{array} \)
\(\begin{array}{l}\Rightarrow m_1 = -\frac {1}{m_2} \end{array} \)
\(\begin{array}{l}\Rightarrow m_1 ~\times ~m_2 = -1\end{array} \)
Таким образом, чтобы две прямые были перпендикулярны, произведение их наклона должно быть равно -1.
Если уравнения двух прямых задаются как ax + by + c = 0 и a’ x + b’ y + c’ = 0, то они перпендикулярны, если aa’ + bb’ = 0. (Опять вы можно прийти к этому результату, если найти наклоны каждой прямой и приравнять их произведение к -1.)
Также читайте: Перпендикулярные линии
Наклон для коллинеарности
Чтобы две прямые AB и BC лежали на одной прямой, наклон обеих прямых должен быть одинаковым и должна быть хотя бы одна общая точка, через которую они должны проходить. Таким образом, чтобы три точки A, B и C лежали на одной прямой, наклоны AB и BC должны быть равны.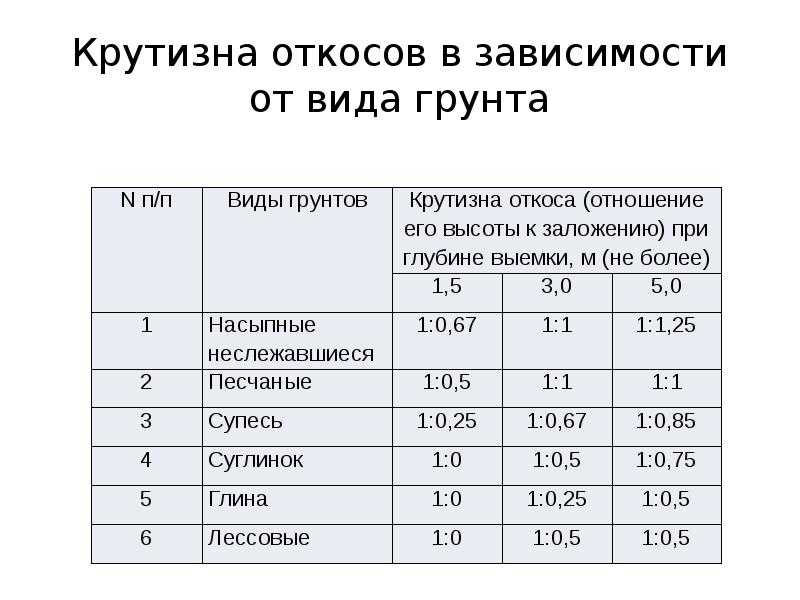
Если уравнение двух прямых задается как ax + by + c = 0 и a’ x+b’ y+c’ = 0, то они коллинеарны, когда ab’ c’ = a’ b’ c = a’ c’b.
Угол между двумя линиями
Когда две прямые пересекаются в одной точке, угол между ними может быть выражен через их наклоны и определяется по следующей формуле:
\(\begin{array}{l}tan\ \theta = | \frac{ m_2~-~m_1}{1~+~m_1~ m_2}|\end{array} \)
где м 1 и м 2 — наклоны линий AB и CD соответственно.
\(\begin{array}{l}\text{Если } \frac{ m_2~-~m_1}{1~+~m_1~ m_2} \text{ положительно, то угол между прямыми острый.}\ конец {массив} \)
\(\begin{array}{l}\text{Если } \frac{ m_2~-~m_1}{1~+~m_1~ m_2} \text{ отрицательно, то угол между линиями тупой.}\ конец {массив} \)
Наклон вертикальных линий
Вертикальные линии не имеют наклона, так как не имеют крутизны. Или можно сказать, что мы не можем определить крутизну вертикальных линий.
Вертикальная линия не будет иметь значений координат x.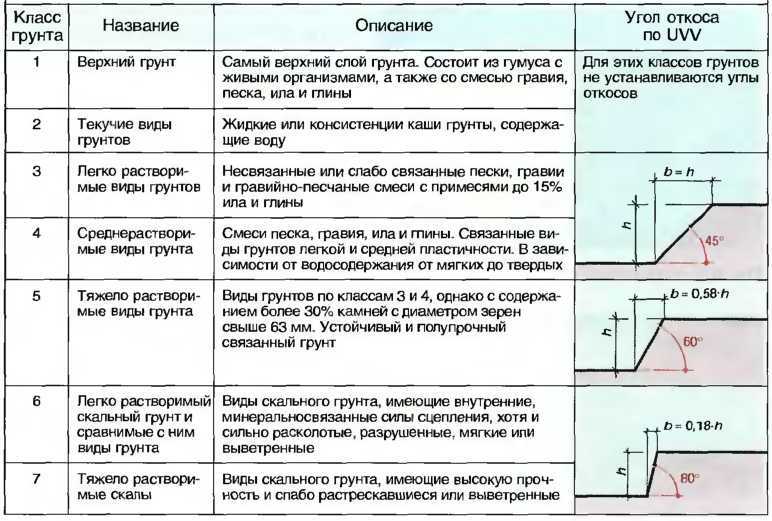 Итак, согласно формуле наклона линии,
Итак, согласно формуле наклона линии,
Уклон, м = (y 2 – y 1 )/(x 2 – x 1 )
Но для вертикальных линий х 2 = х 1 = 0
Следовательно,
м = (у 2 – у 1 )/0 = не определено
Точно так же наклон горизонтальной линии равен 0, так как координаты y равны нулю.
м = 0/(x 2 – x 1 ) = 0 [для горизонтальной линии]
Положительный и отрицательный наклон
Если значение наклона линии положительное, это показывает, что линия поднимается вверх по мере нашего движения или положительное значение подъема над бегом.
Если значение наклона отрицательное, то линия на графике прокручивается, когда мы движемся вдоль оси x.
Решенные примеры наклона линии
Пример 1:
Найдите наклон прямой между точками P = (0, –1) и Q = (4,1).
Решение:
Даны точки P = (0, –1) и Q = (4,1).
Из формулы наклона мы знаем, что
Наклон линии, м = (y 2 – y 1 )/(x 2 – x 1 )
м = (1-(-1))/(4-0) = 2/4 = ½
Пример 2:
Найдите наклон линии между P(–2, 3) и Q(0, –1).
Решение:
Даны две точки P(–2, 3) и Q(0, –1).
Следовательно, наклон линии
м = (-1-3)/0-(-2) = -4/2 = -2
Пример 3:
Рамья проверяла график и поняла, что рейз составил 10 единиц, а пробег — 5 единиц. Каким должен быть наклон линии?
Решение:
Учитывая, что повышение = 10 единиц
Пробег = 5 ед.
Мы знаем, что наклон линии определяется как отношение подъема к пробегу.
т.е. уклон, м = подъем/прогон
Следовательно, наклон = 10/5 = 2 единицы.
Следовательно, наклон линии равен 2 единицам.
Оставайтесь с нами с BYJU’S — приложением для обучения и загрузите приложение, чтобы легко изучать все понятия, связанные с математикой, просматривая больше видео.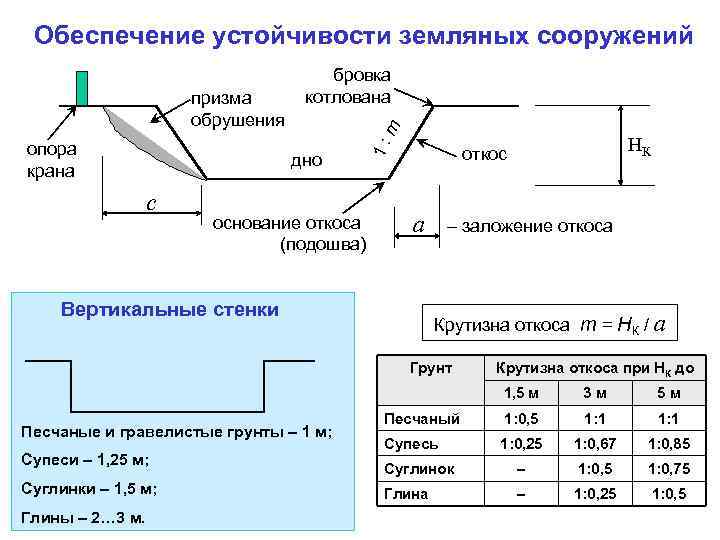

Добавить комментарий