Крутизна откосов котлована и траншей

При возведении фундамента под частный дом большое значение имеет крутизна откосов котлована и траншей.

Устройство котлована

При выборе способа выполнения земляных работ учитывают:

• тип конструкции;
• глубину заложения;
• объем работ.

При сооружении ленточного и столбчатого мелкозаглубленного фундамента грунты могут разрабатываться вручную. При строительстве дома с подвалом или цокольным этажом работы должны быть механизированы.

Выемку основного объема грунта выполняет экскаватор с прямой или обратной лопатой. При этом котлован необходимо отрывать без нарушения плотности грунта в основании фундамента. Чтобы соблюсти данное требование, предусматривают недобор грунта в пределах 5-20 см. Зачистку откосов и выемку грунта с основания до проектной отметки выполняют вручную разнорабочие.

Выбираемый грунт должен сразу же вывозиться или размещаться на строительной площадке на расстоянии более 1 м от края котлована.

Выбор техники зависит от типа грунта, глубины котлована и объема работ. При строительстве частного дома шириной не более 15 м, можно задействовать экскаватор с обратной лопатой с объемом ковша до 1,4 м3 на колесном или гусеничном шасси.

Значение проектирования откосов

Любой грунт, ограниченный откосами, под действием силы тяжести стремится сдвинуться в сторону откоса, что может привести к неконтролируемому обрушению стенок котлована. Из-за обрушения грунтовых масс могут пострадать рабочие, находящиеся на дне котлована. К тому же это приведет к увеличению объема работ и несоблюдению календарного графика. Так как нужно будет восстанавливать проектный контур котлована, и выполнять обратную засыпку фундамента в большем объеме.

Чтобы избежать травм и не нести убытки, необходимо еще на этапе проектирования рассчитать крутизну откосов котлована и траншей, в соответствии со СНиП 111-4-80.

Нормативные данные для проектирования откосов

Устройство котлована с вертикальными без крепления стенками допускается, только при разработке:

• насыпных, песчаных или гравелистых грунтов на глубину не более 1м;
• супесчаных и суглинистых – не более чем на 1,25м;
• глинистых – на 1,5 м;
• особо плотных – на 2 м.

Если же требуется устройство котлована большей глубины, необходимо принять крутизну откосов, рекомендуемую СНиП с учетом типа грунта и глубины заложения. При этом если глубина котлована или траншеи превышает 5 м, то для определения устойчивости земляных масс выполняют расчет.

Крепление стенок котлована глубиной 2-3 м должно выполняться строго по типовому проекту.

В нормативной литературе крутизна откосов котлована и траншей измеряется как угол откоса (ɑ) или отношение высоты откоса к заложению (1:m). В СНиП эти данные приводятся в табличной форме отдельно для каждого типа грунта с учетом глубины выемки.

Если на участке присутствует несколько видов грунта, то крутизну откосов принимают, ориентируясь на самые неустойчивые слои.

В связи с тем, что даже при разработке котлована с откосами не исключена вероятность обрушения грунта под тяжестью машин, необходимо соблюдать требуемое в СНиП расстояние от подошвы откоса до места стояния техники.

Рассчитывая объем земляных работ, учитывают величину откосов, которые увеличивают ширину котлована на b=m*h.

Допускаемая крутизна откосов траншей

Книга отзывов Обратная связь  Группа в Telegram! ! «Сметное дело» ! Число посетителей: Материалы, опубликованные на сайте, взяты из нормативных документов в строительстве, сети интернета и мои разработки, идеи, труды.

Бесплатные программы в помощь Строителям и Сметчикам [67] Инженер-сметчик должен ЗНАТЬ [26] Исполнительная документация в строительстве [12] Исходно-разрешительная документация (ИРД) [6] Контроль качества СМР (Надзор) [16] Все теги Тематическая подборка по заголовку страницы. Пользователи могут комментировать заявленную тему, задавать вопросы по ней и получать ответы, а также сами отвечать на вопросы других пользователей форума и давать им советы. Дополнительная информация по данной теме Страница находится на стадии разработки Допускаемая крутизна откосов траншей Когда выполняются земляные работы (рытье котлована или траншей) нередки случаи образования откосов при осыпании грунта. Крутизна этих откосов зависит от вида грунта и глубины копания.      Ниже представлена таблица, которая поможет вам определить крутизну будущего откоса для расчета объема земляных работ котлована или траншеи. Минимальное расстояние от основания откоса до ближайших опор машины Глубина выемки, м Грунт ненасыпной песчаный супесчаный суглинистый глинистый Расстояние по горизонтали от основания откоса выемки до ближайшей опоры машины, м 1,0 1,5 1,25 1,00 1,00 2,0 3,0 2,40 2,00 1,50 3,0 4,0 3,60 3,25 1,75 4,0 5,0 4,40 4,00 3,00 5,0 6,0 5,30 4,75 3,50   Справочная литература – «Назад | Вперед » Навигация и структура информации на сайте Термины и определения  |  Количество проходов и рациональный режим работы грунтоуплотняющих машин  |  Допускаемая крутизна откосов траншей Версия для печати

Подписка на рассылку Никакого спама !!!

Наклон – определение, типы, примеры

Наклон линии – это мера крутизны и направления линии. Нахождение наклона линий на координатной плоскости может помочь предсказать, параллельны ли линии, перпендикулярны или нет, без фактического использования компаса.

Наклон любой линии можно рассчитать, используя любые две различные точки, лежащие на линии. Формула наклона линии вычисляет отношение «вертикального изменения» к «горизонтальному изменению» между двумя различными точками на линии. В этой статье мы разберемся с методом нахождения уклона и его применениями.

1.	Что такое уклон?
2.	Наклон линии
3.	Наклон линии Формула
4.	Как найти уклон?
5.	Типы уклонов
6.	Наклон перпендикулярных линий
7.	Наклон параллельных линий
8.	Часто задаваемые вопросы о склоне

Что такое уклон?

Наклон линии определяется как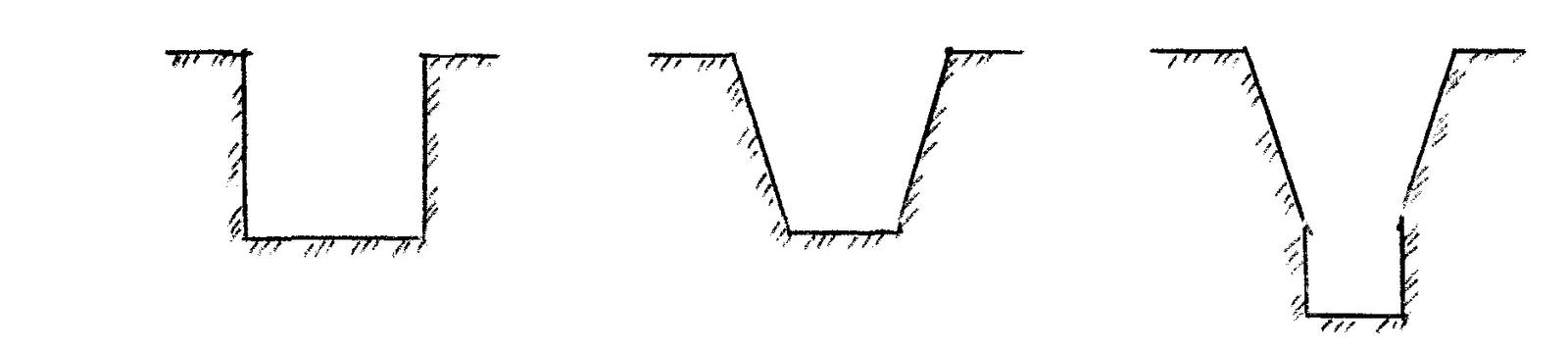

изменение координаты y по отношению к изменению координаты x этой линии . Чистое изменение координаты y равно Δy, а чистое изменение координаты x равно Δx. Таким образом, изменение координаты y по отношению к изменению координаты x можно записать как

м = Δy/Δx
где м — уклон

Обратите внимание, что тангенс θ = Δy/Δx

Мы также называем этот тангенс θ наклоном линии.

Наклон линии

Наклон линии представляет собой отношение подъема к пробегу или подъема, деленное на пробег. Он описывает крутизну линии в координатной плоскости. Вычисление наклона линии аналогично нахождению наклона между двумя разными точками. В общем, чтобы найти наклон линии, нам нужно иметь значения любых двух разных координат на линии.

Наклон между двумя точками

Наклон линии можно рассчитать, используя две точки, лежащие на прямой. Зная координаты двух точек, мы можем применить формулу наклона линии. Пусть координаты этих двух точек будут

. Р ₁ = (х ₁ , у ₁ )
P ₂ = (x ₂ , y ₂ )

Как мы обсуждали в предыдущих разделах, наклон представляет собой «изменение координаты y по отношению к изменению координаты x этой линии». Итак, подставляя значения Δy и Δx в уравнение наклона, мы знаем, что:
Δу = у ₂ – у ₁
Δx = x ₂ – x ₁

Следовательно, используя эти значения в соотношении, мы получаем: – x ₁ )

где m — наклон, а θ — угол, образуемый линией с положительной осью x.

Формула наклона линии

Наклон линии можно рассчитать по уравнению линии. Общий наклон формулы линии задается как

y = mx + b

где

• м — уклон, такой, что m = tan θ = Δy/Δx
• θ — угол, образуемый линией с положительной осью x
• Δy — чистое изменение по оси Y
• Δx — чистое изменение по оси x

Наклон линии Пример

Вспомним определение наклона линии и попробуем решить приведенный ниже пример.

Пример: Уравнение линии с наклоном 1, проходящей через точку (-1, -5) ?

Решение:

Мы знаем, что если уклон равен 1, то значение м будет равно 1 в общем уравнении y = mx + b.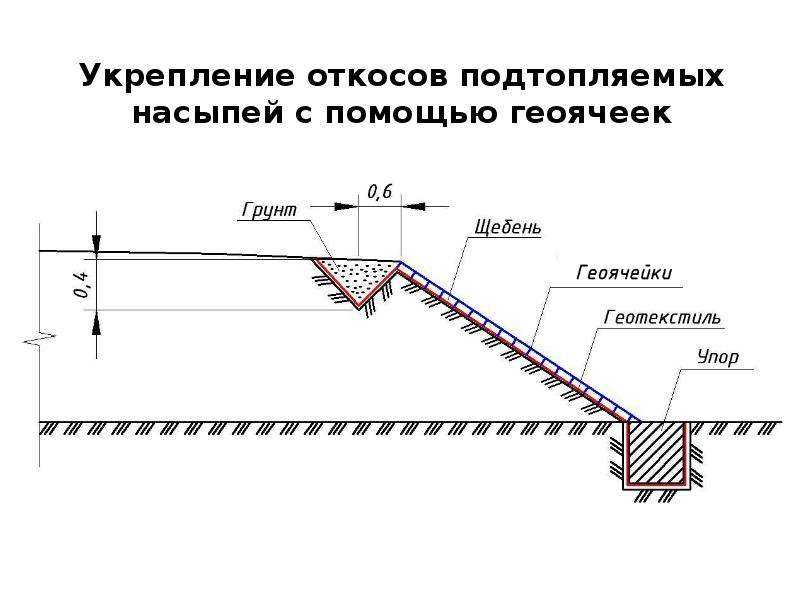 Итак, подставляем значение м в 1, и получаем

y = x + b

Теперь у нас уже есть значение одной точки на прямой. Итак, подставляем значение точки (-1, -5) в уравнение y = x + b, и получаем,

b = -4

Отсюда, подставляя значения

m и b в общем уравнении, мы получаем наше окончательное уравнение как y = x – 4.

Уравнение: y = x – 4

Как найти уклон?

Наклон линии можно найти разными способами. Первый метод определения значения уклона заключается в использовании уравнения, которое задается следующим образом: где m – наклон линии.

Кроме того, изменение x равно запустить и изменить y рост или падение . Таким образом, мы также можем определить наклон как m = подъем/спуск

Нахождение наклона на графике

Один из методов нахождения наклона линии на графике заключается в непосредственном применении формулы с учетом координат двух лежащих точек. на линии. Допустим, значения координат двух точек не заданы. Итак, у нас есть еще один способ найти наклон линии. В этом методе мы пытаемся найти тангенс угла, образованного линией с осью x. Следовательно, мы находим наклон, как указано ниже.

Наклон линии имеет только одно значение. Таким образом, наклоны, найденные методами 1 и 2, будут равны. В дополнение к этому, скажем, нам дано уравнение прямой линии. Общее уравнение линии может быть дано как

y = mx + b

Значение уклона дано как м; , следовательно, значение м дает наклон любой прямой.

Следующие шаги можно выполнить, чтобы найти наклон прямой, такой, что координаты двух точек, лежащих на прямой, равны: (2, 4), (1, 2)

• Шаг 1: Запишите координаты двух точек, лежащих на прямой, (x ₂ , y ₂ ), (x ₁ , y ₁ ). Здесь координаты даны как (2, 4), (1, 2).
• Шаг 2: Примените формулу наклона линии, m = (y ₂ – y ₁ )/(x ₂ – x ₁ ) = (4 – 2)/(2 – 1) = 2,
• Шаг 3: Следовательно, наклон данной линии = 2.

Типы уклонов

Мы можем классифицировать наклон по различным типам в зависимости от отношения между двумя переменными x и y и, таким образом, от значения градиента или наклона полученной линии. Существует 4 различных типа уклонов, обозначенных как

• Положительный уклон
• Отрицательный наклон
• Нулевой наклон
• Неопределенный уклон

Положительный наклон

Графически положительный наклон указывает на то, что при движении слева направо в координатной плоскости линия поднимается, что также означает, что при увеличении x увеличивается и y.

Отрицательный наклон

Графически отрицательный наклон указывает на то, что при движении слева направо в координатной плоскости линия падает, что также означает, что при увеличении x уменьшается y.

Нулевой наклон

Для линии с нулевым наклоном подъем равен нулю, и, таким образом, применяя формулу превышения подъема, мы получаем нулевой наклон линии.

Неопределенный уклон

Для линии с неопределенным уклоном значение длины равно нулю. Наклон вертикальной линии не определен.

Наклон горизонтальной линии

Мы знаем, что горизонтальная линия — это прямая линия, параллельная оси x или проведенная слева направо или справа налево в координатной плоскости. Следовательно, чистое изменение координаты y горизонтальной линии равно нулю. Наклон горизонтальной линии можно определить как

Наклон горизонтальной линии, m = Δy/Δx = ноль

Наклон вертикальной линии

Мы знаем, что вертикальная линия — это прямая линия, параллельная оси Y или рисуется сверху вниз или снизу вверх в координатной плоскости. Следовательно, чистое изменение координат x вертикальной линии равно нулю. Наклон вертикальной линии можно определить как

Наклон вертикальной линии, м = Δy/Δx = не определено

Наклон перпендикулярных линий

Набор перпендикулярных линий всегда имеет между собой угол 90º. Предположим, что у нас есть две перпендикулярные линии l ₁ и l ₂ в координатной плоскости, наклоненные под углами θ ₁ и θ ₂ соответственно с осью x, так что данные углы следуют внешнему углу теорема как, θ ₂ = θ ₁ + 90º.

Следовательно, их наклоны можно представить как
м ₁ = тангенс θ ₁
м ₂ = загар (θ ₁ + 90º) = – раскладушка θ ₁
⇒ m ₁ × m ₂ = -1

Таким образом, произведение наклонов двух перпендикулярных прямых равно -1.

Наклон параллельных линий

Набор параллельных линий всегда имеет одинаковый угол наклона. Предположим, у нас есть две параллельные линии l ₁ и l ₂ в координатной плоскости, наклоненные под углом θ ₁ и θ ₂ соответственно с осью x, так что θ ₂ = θ ₁ .

Следовательно, их наклоны могут быть указаны как
⇒ m ₁ = m ₂

Таким образом, наклоны двух параллельных прямых равны.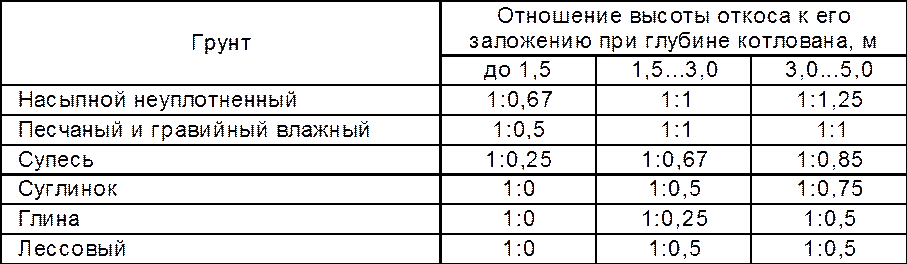

Важные примечания по наклону:

• Наклон линии — это мера тангенса угла, образуемого линией с осью x.
• Наклон постоянен на протяжении всей прямой.
• Форма пересечения наклона прямой линии может быть задана как y = mx + b
• Наклон обозначается буквой m и определяется выражением m = tan θ = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Сложный вопрос:

Прямая имеет уравнение y = 2x – 7. Найдите уравнение прямой, перпендикулярной данной прямой и проходящей через начало координат.

☛ Похожие темы:

• Линейное уравнение
• Квадратное уравнение
• Кубическое уравнение

Часто задаваемые вопросы о склоне

Что такое наклон линии?

Наклон линии, также известный как градиент, определяется как значение крутизны или направление линии в координатной плоскости. Уклон можно вычислить разными способами, зная уравнение прямой или координаты точек, лежащих на прямой.

По какой формуле можно найти наклон линии?

Мы можем рассчитать наклон линии напрямую, используя формулу наклона линии, зная координаты двух точек, лежащих на линии. Формула дается как,
Уклон = m = tan θ = (y ₂ – y ₁ )/(x ₂ – x ₁ )

Как рассчитать уклон?

Наклон определяется путем измерения тангенса угла, образованного линией с осью x. Существуют различные методы определения наклона линии. Выражение, которое можно использовать для определения наклона, имеет вид tan θ или (y ₂ – y ₁ )/(x ₂ – x ₁ ), где θ – угол, который линия образует с положительной осью x, и (x ₁ , y ₁ ) и (x ₂ , y ₂ ) — координаты двух точек, лежащих на прямой.

Какие существуют 4 типа склонов?

Существует 4 различных типа наклона: положительный наклон, отрицательный наклон, нулевой наклон и неопределенный наклон.

Что такое неопределенный уклон?

Любой уклон с углом 90º с осью x, будет иметь неопределенное значение тангенса 90º. Следовательно, такие линии будут иметь неопределенное значение наклона.

Как выглядит склон?

Наклон — это не что иное, как мера тангенса угла, составленного с осью x. Следовательно, это всего лишь мера угла.

Какие 3 способа найти уклон?

Способы определения уклона: форма точечного уклона, форма пересечения уклона и стандартная форма. Мы можем применить любую из форм уравнения прямой линии, учитывая необходимую информацию, чтобы найти наклон.

Как показать, что три точки лежат на одной прямой по наклону?

Чтобы доказать коллинеарность трех точек, скажем, A, B и C, мы можем применить формулу наклона. Наклон прямых AB и BC должен быть одинаковым, чтобы три заданные точки были точками на одной прямой.

Как найти уклон по двум точкам?

Наклон можно рассчитать, используя координаты двух точек по формуле m = (y ₂ – y ₁ )/(x ₂ – x ₁ ), где (x ₁ , y ₁ ) и (x ₂ , y ₂ ) — координаты двух точек, лежащих на прямой.

Определение наклона — понятие

Одна из самых важных идей, которые вы
встретите во всем своем изучении
алгебры, — это понятие наклона.
И наклон просто относится к
насколько крута линия.
Это основное определение.
Это то, что я помогаю — или помогает
мне вспомнить, что означает уклон.

Много причудливых обозначений
, который идет вместе с ним.
И мы поговорим об этом через секунду.
Но если вы
задним числом вспомните, что наклон означает, насколько
крута линия, это
вам очень поможет.

Итак, вы видите, что каждый раз, когда я
рисую прямую линию, коэффициент наклона
остается одинаковым для всей этой линии.
И вот что я имею в виду.

Допустим, это мои оси X и Y
, и у меня есть вот эта линия.
Линия одинаково крутая
все время.
Имеет тот же коэффициент наклона.
И мы собираемся получить второе
то, что я имею в виду под отношением.
И вот о чем я говорю.
Когда мы говорим об уклоне или крутизне,
определяется как изменение
Y по сравнению с изменением X. Как
в дроби.
Изменение Y сверх изменения X.
Вот почему мы называем это соотношением.

Помните, что соотношение похоже на дробь.
Итак, если бы я нарисовал здесь маленький треугольник
, который показывает, насколько крута моя линия
, это будет моя замена в части Y
, потому что Y вверх и вниз.
Это будет мое изменение в части X,
, потому что X расположен горизонтально.
И какими бы ни были эти числа на графике
, я бы написал в виде дроби.
Это одна вещь, которую
должен помнить.
Изменение Y поверх изменения X.

Иногда мы пишем это, используя этот маленький треугольник
.
Этот треугольник представляет собой греческую букву
дельта, что сложно.
Вам нужно не только учить математику
но теперь вам нужно выучить греческий.
Это означает изменение в Y поверх изменения
в X. Эта
дельта представляет собой просто изменение слова.

И третий способ написать это, используя
букву М. М означает наклон,
и если бы у меня было две точки,
я использовал бы их здесь.
Допустим, у меня есть эта точка. Я собираюсь
назвать ее X из моей первой точки, а затем
Y из моей первой точки.
Вот мое второе замечание.
X из моей второй точки. Я собираюсь использовать
, эту маленькую 2, чтобы показать, что это моя вторая 9.0071 точка. Y для моего второго пункта.

Тогда есть формула, которую я мог бы использовать, используя
эти числа X и Y, чтобы найти M, или
наклон.
И так я бы написал, что Y на
убрать Y1 поверх X2 убрать X1.
Это то же самое, только
написано по-другому.
Я выясняю, насколько изменились мои значения Y
, и добавляю это к тому, насколько
сильно изменились мои значения X
в дробях.

Так что эта формула всегда актуальна
у вас есть две точки, как это.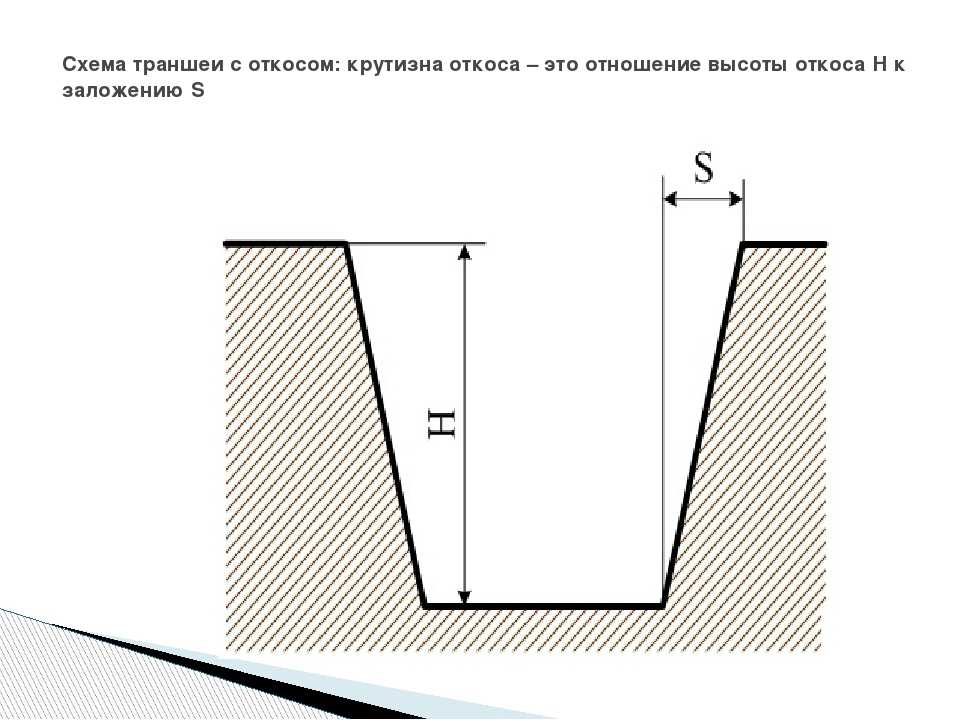
Эти маленькие числа здесь хитрые.
Это не значит взять ваше значение Y и
умножить его на 2 или взять ваше значение Y
и умножить его на 1. Это означает, что
это то, что мы просто записываем с помощью
то, что называется индексом.
Это мое второе значение Y.
Я вычитаю свое первое значение Y.
И мы вернемся к этому позже, когда вы,
, ребята, приступите к домашним заданиям.

Еще пара вещей, которые я хочу, чтобы вы помнили о
с наклоном, а это
иногда наклоны — это положительные числа
, а иногда наклоны — отрицательные числа
. И вот как вы можете сказать.

Каждый раз, когда вам дают график,
есть моя ось и моя линия.
Подумайте, если бы вы катались на скейтборде
, и вы двигались бы вперед, и вы бы
врезались в эту рампу.
Это пандус в гору.
Мы называем это положительным наклоном.
В отличие от того, если вы ударите по этой линии здесь,
здесь вы идете по скейтборду,
Я не знаю, почему это шум скейтбординга.
Я только что это придумал. Ты катаешься на скейтборде.
Если вы ударите эту штуку, вы упадете.
Вот почему мы называем это отрицательным наклоном.
Всякий раз, когда линия увеличивается слева
вправо, это называется положительным.
Уменьшается слева направо,
называется минусом.

О многом нужно помнить, когда
вы, ребята, подходите к своим проблемам.
Это все математические обозначения, которые
вы будете видеть снова и снова и
снова и снова.
Так что привыкнешь.

Последнее, что я хочу оставить вам,
, это размышления о задачах со словами,
потому что во многих случаях графики, как мы
знаем, представляют реальный мир.
Например, этот график может отображать рост в день,
или то, насколько что-то изменилось за
раз.

Таким образом, наклон становится действительно важным, когда
вы смотрите на текстовые задачи.
Это может быть прирост в день.
Допустим, мой наклон равен 5.