Автомобильные рессоры могут иметь жесткость порядка 2 10: №499. Автомобильные рессоры могут иметь жесткость порядка 2 • 104 Н/м. Каков будет период колебаний, если на рессоры упадет груз массой 500 кг?
Решение задач по теме «Механические колебания»
Материал опубликовала
19
#9 класс #Физика #Методические разработки #Урок #Учитель-предметник #Школьное образование #УМК А. В. Пёрышкина
Нажмите, чтобы скачать публикацию
в формате MS WORD (*.DOC)
Размер файла: 33.75 Кбайт
План- конспект урока физики в 9 классе
Решение задач по теме « Механические колебания»
Цель урока: Закрепить основные понятия, формулы, продолжить формирование навыков решения задач.
Ход урока.
1.Орг. момент
Урок начинаем со стихотворения Н.А.Заболоцкого «Утро»
Рожденный пустыней,
Колеблется звук,
Колеблется синий
На ветке паук.
Колеблется воздух,
Прозрачен и чист,
В сияющих звездах
колеблется лист.
-Скажите, о чем сегодня пойдет речь? (о колебаниях)
2. Повторение.
Повторение.
1)Исключите лишнее:
А)амплитуда, период, частота, маятник;
Б) Гц, с-1; с;
В) …=1/Т; …=n/t; …= ; …=…=
( ответ: …= )
2)Найдите ошибку.
А) а=F/m ; Б) Т= ; В)Т= n/t; Г) v= n/t .
( ответ: Б)
3) Подберите обобщающее слово
А) колебания- …. (обобщающее слово-движение)
Б) период-….. (время)
В) частота-… (число колебаний)
Г) секундомер-… (прибор)
4)Рассыпанное предложение
Приближенно, или, движения, колебания, точно, которые ,это, повторяются.
5)Выделите из прибора устройство, связанное с колебательным процессом:
С М Е А К Я У Т Н Н Д И О К М Е Р
( секундомер, маятник)
3.Решение задач.
1) На рисунке представлена зависимость координаты центра шара, подвешенного на пружине ,от времени. Определите период и частоту колебаний.
Ответ: 4с; 0,25Гц.
2)Амплитуда свободных колебаний тела равна 0,5м.Какой путь прошло это тело за 5 периодов колебаний?
Ответ: 10м.
3) Ворона за 3 мин каркнула 45 раз. Вычислите частоту и период раскрывания клюва вороны.
Ответ: 0,25Гц, 4с.
4) У одного очень болтливого мальчишки язык за 10 мин совершил 2400 колебаний. Вычислите частоту и период колебаний языка этого болтуна.
Ответ: 4Гц; 0,25с
5)Автомобильные рессоры могут иметь жесткость порядка 2·104 Н/м. Каков будет период колебаний, если на рессоры упадет груз массой 500 кг?
Ответ: 1с.
4.Итог урока.
5.Рефлексия.
На столах у учащихся листочки с началами фраз.
Допишите предложения:
– сегодня я узнал(а)…
– было трудно…
– я понял(а), что…
– я научился(лась)…
– я смог(ла)…
– было интересно узнать, что…
– меня удивило…
– мне захотелось узнать
Литература и интернет –ресурсы
1.Громцева, О.И.Контрольные и самостоятельные работы по физике.9класс: к учебнику А.В.Перышкина, Е.М. Гутник «Физика 9 класс» / О. И. Громцева.-2-у исправл.-М.:Издательство «Экзамен»,2010
И. Громцева.-2-у исправл.-М.:Издательство «Экзамен»,2010
2.Сборник задач по физике: Для 10-11кл.общеобразоват.учреждений/ Сост.Г.Н.Степанова.-8-е изд.- М.:Просвещение,2002.
http://www.pedsovet.pro /
Опубликовано
власова Наталья Николаевна, 06.07.17 в 11:06 4ОтветитьПожаловаться
Спасибо за идею “рассыпанное предложение”.
Горбачёва Марина Юрьевна, 17.09.18 в 15:01 5ОтветитьПожаловаться
Интересная работа!
Трефилова Раиса Поликарповна, 12.01.19 в 20:55 5ОтветитьПожаловаться
Спасибо за представленный опыт работы!!!
Горбачёва Марина Юрьевна, 13.01.19 в 06:54 1ОтветитьПожаловаться
Задач много не бывает!
Чтобы написать комментарий необходимо авторизоваться.
Автор публикации: Янченко И.А. Дата публикации: 2016-09-21 Краткое описание: … Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 7
Вариант 8
Вариант 9
Вариант 10
Вариант 11
|
Как рассчитать константу пружины с помощью закона Гука
Любой физик знает, что если объект прикладывает силу к пружине, то пружина прикладывает к объекту равную и противоположную силу. Закон Гука дает силу, с которой пружина действует на прикрепленный к ней объект, с помощью следующего уравнения:F = – kx
Знак минус показывает, что эта сила направлена в противоположную сторону от силы, которая растягивает или сжимает весна. Переменные уравнения F, , которое представляет силу, k, , которое называется жесткостью пружины и измеряет, насколько жесткой и прочной является пружина, и x, расстояние, на которое пружина растягивается или сжимается от своего положения равновесия или покоя.
Переменные уравнения F, , которое представляет силу, k, , которое называется жесткостью пружины и измеряет, насколько жесткой и прочной является пружина, и x, расстояние, на которое пружина растягивается или сжимается от своего положения равновесия или покоя.
Сила, действующая на пружину, называется возвращающей силой; он всегда действует, чтобы вернуть пружину к равновесию. В законе Гука отрицательный знак силы пружины означает, что сила, действующая на пружину, противодействует смещению пружины.
Понимание пружин и направления их действия
Направление силы пружины
На предыдущем рисунке показан шарик, прикрепленный к пружине. Вы можете видеть, что если пружина не растягивается и не сжимается, она не действует на шарик. Однако если вы нажмете на пружину, она оттолкнется назад, а если вы потянете пружину, она оттянется назад. Закон Гука действует до тех пор, пока эластичный материал, с которым вы имеете дело, остается эластичным, то есть остается в пределах предела эластичности . Если вы потянете пружину слишком далеко, она потеряет способность растягиваться. Пока пружина остается в пределах своего предела упругости, можно сказать, что F = – kx . Когда пружина остается в пределах своего предела упругости и подчиняется закону Гука, пружина называется идеальной пружиной .
Если вы потянете пружину слишком далеко, она потеряет способность растягиваться. Пока пружина остается в пределах своего предела упругости, можно сказать, что F = – kx . Когда пружина остается в пределах своего предела упругости и подчиняется закону Гука, пружина называется идеальной пружиной .
Как найти жесткость пружины (пример задачи)
Предположим, к вам в дверь стучится группа дизайнеров автомобилей и спрашивает, не могли бы вы помочь спроектировать систему подвески. «Конечно, — говорите вы. Вам сообщают, что машина будет иметь массу 1000 кг, и вам предстоит работать с четырьмя амортизаторами длиной по 0,5 метра каждый. Насколько сильными должны быть пружины? Если предположить, что в этих амортизаторах используются пружины, каждый из них должен выдерживать массу не менее 250 кг, что соответствует следующему весу:F = мг = (250 кг)(9,8 м/с 2 ) = 2450 Н
где F равно силе, м равно массе 4 г и 9000 ускорение свободного падения, 9,8 метра в секунду 2 . Пружина в амортизаторе должна, как минимум, дать вам усилие в 2450 ньютонов при максимальном сжатии 0,5 метра. Что это означает, что жесткость пружины должна быть? Чтобы выяснить , как рассчитать жесткость пружины , мы должны помнить, что говорит закон Гука:
Пружина в амортизаторе должна, как минимум, дать вам усилие в 2450 ньютонов при максимальном сжатии 0,5 метра. Что это означает, что жесткость пружины должна быть? Чтобы выяснить , как рассчитать жесткость пружины , мы должны помнить, что говорит закон Гука:
F = – kx
Теперь нам нужно переработать уравнение так, чтобы мы вычисляли недостающую метрику, которая является постоянной пружины, или k . Глядя только на величины и, следовательно, опуская отрицательный знак, вы получаете
Время подставить числа:
Пружины, используемые в амортизаторах, должны иметь жесткость не менее 4900 ньютонов на метр. Автомобильные дизайнеры выбегают в восторге, но вы кричите им вдогонку: «Не забывайте, вам нужно как минимум удвоить это, если вы действительно хотите, чтобы ваша машина могла преодолевать выбоины».
Об этой статье
Эта статья из книги:
- Физика I для чайников,
Об авторе книги:
Доктор Стивен Хольцнер написал более 40 книг по физике и программированию. Он был редактором журнала PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором книг для чайников, в том числе Physics For Dummies и Physics Essentials For Dummies. Доктор Хольцнер получил докторскую степень в Корнелле.
Он был редактором журнала PC Magazine и преподавал в Массачусетском технологическом институте и Корнелле. Он является автором книг для чайников, в том числе Physics For Dummies и Physics Essentials For Dummies. Доктор Хольцнер получил докторскую степень в Корнелле.
Эту статью можно найти в категории:
- Физика ,
Расчет идеальной жесткости пружины и поперечной балки – Как отрегулировать и настроить – Секреты подвески
Скорость движения и крена вашего автомобиля определяют замену колеса нагрузки к изменению положения тела, будь то в кочках или кувырках. Коэффициенты крена определяют изменение нормальной силы шины из стороны в сторону при заданном крутящем моменте, приложенном к шасси, или заданной величине крена шасси. Скорость движения определяет изменение нормальной силы шины для одного колеса в чисто вертикальное изменение положения тела.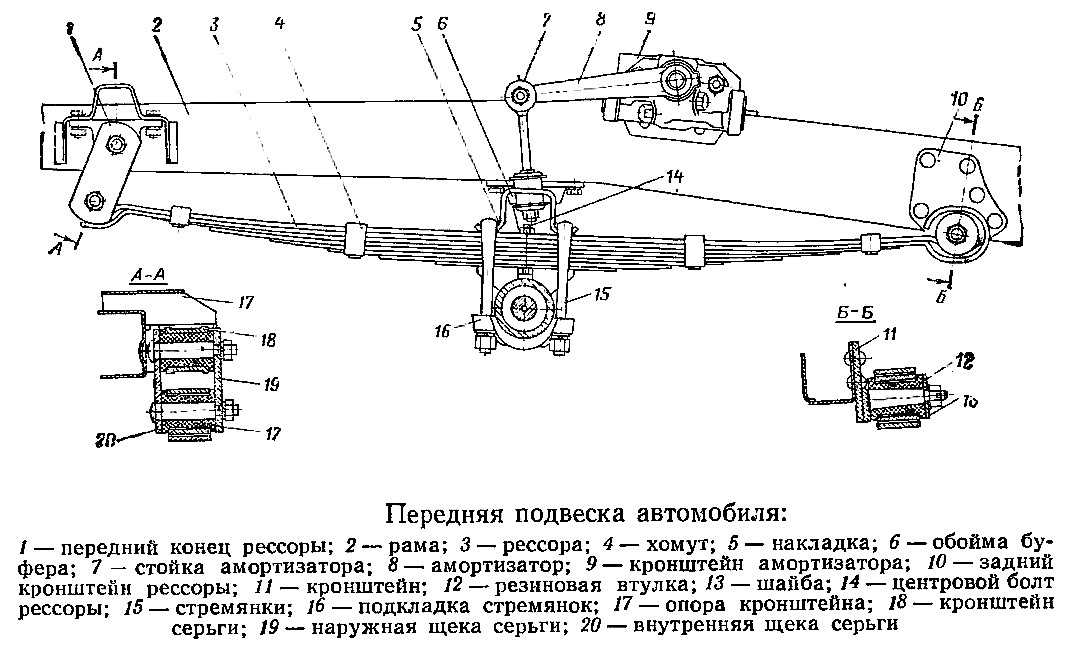
Одной из основных целей подвески является обеспечение максимального сцепления шин с дорогой, чтобы автомобиль ехал как можно быстрее. Есть и другие применения в других секторах автомобилестроения, такие как комфорт, лежачие полицейские и т. Д., Но в этом разделе мы сосредоточимся на гоночных автомобилях и транспортных средствах для автоспорта, которым необходимо только обеспечить максимальное сцепление с автомобилем.
Одна из проблем при расчете идеальной жесткости пружин для автомобиля заключается в том, что расчеты основаны на идеальных нагрузках на колеса автомобиля. Однако для расчета идеальных нагрузок на колеса требуются идеальные жесткости пружин. Таким образом, формируется типовая проектная задача. Чтобы преодолеть это, нам нужно сначала предположить некоторые аспекты системы подвески, к которым мы сможем вернуться, как только у нас будут наши первоначальные цифры для точной настройки.
В этом разделе нам придется сделать некоторые предположения, которые будут объяснены далее.
Этап 1: Допущения
Исходные допущения в этом разделе заключаются в том, что автомобиль имеет нулевой угол развала и что этот развал не меняется во время езды. Это необходимо, чтобы избежать разработки очень сложных уравнений в этом разделе. Мы также должны предположить, что боковая деформация шины не происходит. Прежде всего, необходимо определить скорость движения для системы подвески.
Чтобы получить начальную скорость движения, вы можете начать либо с желаемой частоты, либо с максимального хода, деленного на максимальную нагрузку. Любой вариант будет работать точно. Обычно лучше всего сделать подвеску как можно более мягкой с учетом нагрузки автомобиля, сил на поворотах, жесткости по крену и распределения жесткости по крену. Гоночные автомобили известны своей жесткостью; несмотря на то, что они жесткие, они настолько мягкие, насколько это возможно, и в то же время обеспечивают хорошие характеристики прохождения поворотов, оптимальную нагрузку на колеса и полный диапазон подвески/демпфера для максимально эффективной работы подвески. Для аэромобилей подвеска часто намного жестче, чтобы избежать постоянного изменения высоты дорожного просвета, влияющего на прижимную силу автомобиля.
Для аэромобилей подвеска часто намного жестче, чтобы избежать постоянного изменения высоты дорожного просвета, влияющего на прижимную силу автомобиля.
Уравнение, приведенное ниже, можно использовать для определения оптимальной частоты без демпфирования на основе доступного движения колеса, доступного при ударах и падениях от высоты дорожного просвета. Чтобы проверить ваши результаты или использовать следующие предположения для вашего автомобиля, приведенные ниже цифры были получены из данных автоспорта и могут использоваться в качестве эмпирического правила для вашей категории автомобиля.
Если у вас есть идеальное вертикальное движение колеса при подъеме и опускании, то для преобразования его в частоту можно использовать приведенное ниже уравнение:
Где:
ω = Частота в циклах в минуту
x = Вертикальное смещение колеса относительно дорожного просвета в метрах
Типичная частота движения:
- Легковые автомобили: 30-50 циклов в минуту
- Спортивные автомобили: 70-90 циклов в минуту
- Формула с открытыми колесами без эффекта земли: 95–120 циклов в минуту
- Транспортные средства с высоким эффектом грунта: несколько сотен циклов в минуту в зависимости от уровня прижимной силы.

В качестве альтернативы можно использовать цифры, которые можно использовать для ожидаемого хода колес в классах транспортных средств:
- Легковые автомобили: +/- 10 см
- Спортивные автомобили и автомобили с открытыми колесами без высокой прижимной силы: от +/- 4 см до +/- 8 см
- Автомобиль с высоким уровнем влияния земли: +/- 1,5 см или иногда меньше.
Теперь нам нужно сгенерировать фигуру для работы с нашим градиентом ролла. Градиент крена автомобиля – это количество градусов крена, создаваемое на грамм поперечного ускорения. Опять же, мы можем использовать некоторые типичные значения из данных автоспорта, показанных ниже, чтобы запустить процесс.
Стандартный градиент крена автомобилей:
- Крупногабаритные легковые автомобили: 7,0 град/г
- Маленькие легковые автомобили: 5,0 град/г
- Спортивные автомобили: 4,2 град/г
- Высокопроизводительные дорожные автомобили и автомобили для трековых гонок: 3,0 градуса/г
- Специально построенные гоночные автомобили: 1,5 градуса/г
- Жесткость с активным сервоуправлением: 0 градусов крена или максимально близко к
Теперь мы должны собрать некоторые данные об автомобиле, чтобы начать вычисления с использованием вышеуказанных значений. Первый запуск уравнений будет на автомобиле с независимой подвеской. Решение, которое работает ниже, представляет собой систему с открытым циклом, в которой первоначальные предположения должны быть сначала сделаны и обработаны. Первый сет, скорее всего, будет немного неверным, поэтому мы можем повторно запустить его с измененными цифрами, основанными на нашем первом результате, чтобы приблизиться к идеальной скорости езды и крена.
Первый запуск уравнений будет на автомобиле с независимой подвеской. Решение, которое работает ниже, представляет собой систему с открытым циклом, в которой первоначальные предположения должны быть сначала сделаны и обработаны. Первый сет, скорее всего, будет немного неверным, поэтому мы можем повторно запустить его с измененными цифрами, основанными на нашем первом результате, чтобы приблизиться к идеальной скорости езды и крена.
Условия, которые мы собираемся принять для нашей машины, перечислены ниже. Этот автомобиль симметричен влево/вправо и имеет независимую подвеску. Аэродинамическая подъемная сила, коэффициенты момента качения, крутящий момент трансмиссии и продольное ускорение равны нулю для этой точной точки исследования в средней части поворота. Автомобиль имеет следующие данные:
Вес:
- W1 = 460 кг
- W2 = 460 кг
- W3 = 310 кг
- W4 = 310 кг
Следовательно:
- Вт (спереди) =920 кг
- Вт (сзади) = 620 кг
- Вт (всего) = 1540 кг
Требуемые размеры:
- Ширина передней гусеницы (тс) = 1,5 м
- Ширина задней гусеницы (tr) = 1,5 м
- Колесная база (Д) = 2,9 м
- Высота центра тяжести (h) = 0,457 м
- Центр тяжести относительно высоты оси вращения (H) = 0,335 м
Условия прохождения поворотов:
- Направление поворота = левостороннее
- Радиус прохождения поворота (R) = -180 м
- Скорость прохождения поворотов = 100 миль в час = 44,7 м/с
Высота оси крена над землей:
- Высота передней оси крена (Zrf) = 0,0762 м
- Высота задней оси ролика (Zrr) = 0,1905 м
Возникает нулевой момент привода и продольное ускорение:
- Крутящий момент привода (Td) = 0
- Продольное ускорение (Ax) = 0
Теперь, в качестве заключительного этапа получения цифр, нам нужно принять следующие скорости качки для нашей машины.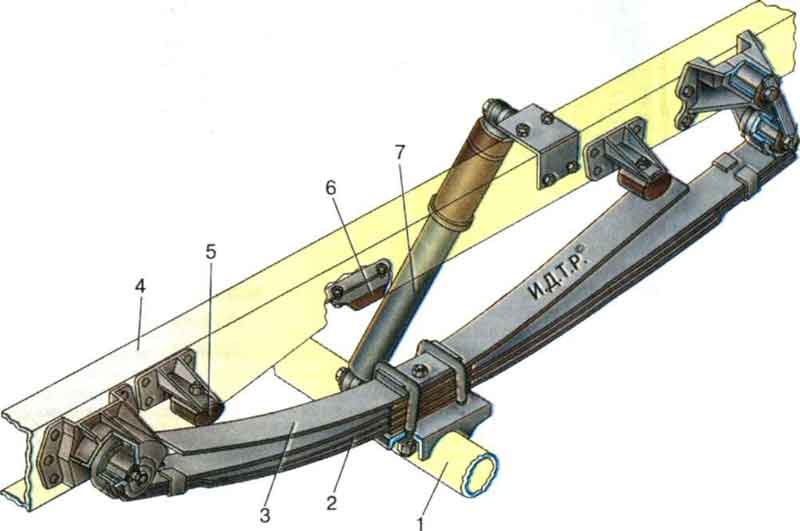 Если у вас переднеприводный автомобиль, выберите более жесткую скорость крена сзади и более мягкую скорость крена спереди. Если у вас заднеприводный автомобиль, как в нашем примере, выберите более мягкую скорость крена сзади и более жесткую скорость крена спереди. Это поможет выгодно распределить скорости передачи нагрузки для вашей установки. Скорость вращения, с которой вы начинаете, не обязательно должна быть точно правильной, поскольку значения будут меняться во время итераций, чтобы отточить правильный результат для вашей настройки.
Если у вас переднеприводный автомобиль, выберите более жесткую скорость крена сзади и более мягкую скорость крена спереди. Если у вас заднеприводный автомобиль, как в нашем примере, выберите более мягкую скорость крена сзади и более жесткую скорость крена спереди. Это поможет выгодно распределить скорости передачи нагрузки для вашей установки. Скорость вращения, с которой вы начинаете, не обязательно должна быть точно правильной, поскольку значения будут меняться во время итераций, чтобы отточить правильный результат для вашей настройки.
На приведенном ниже графике показаны примерные значения поперечной жесткости шасси, которые можно использовать в качестве ориентира для начала в зависимости от массы вашего автомобиля и категории автомобиля, к которой относится ваш автомобиль. Если у вас есть автомобиль, ориентированный на трек, который стремится стать специально построенным гоночным автомобилем, выберите точку между двумя строками категории для веса вашего автомобиля, которая лучше всего описывает вашу настройку. Это значение предназначено только для начала процесса и может меняться с итерациями в ходе процесса, описанного ниже, поэтому не беспокойтесь о том, что ваш выбор будет слишком точным.
Это значение предназначено только для начала процесса и может меняться с итерациями в ходе процесса, описанного ниже, поэтому не беспокойтесь о том, что ваш выбор будет слишком точным.
Масса нашего автомобиля составляет 1540 кг, и он разработан как специально построенный гоночный автомобиль, что соответствует 162700 Нм/радиан на графике. Затем необходимо принять решение о том, как разделить общую скорость крена шасси между передней и задней осями. Так как наш пример с задним приводом и передним расположением двигателя, мы собираемся придать передним колесам более высокую скорость крена, чем задним, чтобы оптимизировать сцепление задних колес. Для нашего примера мы собираемся разделить скорость крена примерно 58/42 между нашими передними и задними колесами, что даст следующие значения для нашей первой итерации.
- Скорость переднего крена (Kφf) = 94900 Нм/радиан = 1656,3 Нм/градус
- Скорость заднего крена (Kφr) = 67800 Нм/радиан = 1183 Нм/градус
Из-за того, что мы еще не знаем скорости движения, мы также не знаем скорости качки, поскольку они зависят друг от друга. Поэтому нам нужно принять скорости качки, чтобы сдвинуться с мертвой точки для расчетов. Мы также должны начать процесс со статических значений центров крена, поскольку они меняются с изменением дорожного просвета и угла крена и т. д.
Поэтому нам нужно принять скорости качки, чтобы сдвинуться с мертвой точки для расчетов. Мы также должны начать процесс со статических значений центров крена, поскольку они меняются с изменением дорожного просвета и угла крена и т. д.
Этап 2: Расчеты
Первый этап расчетов заключается в расчете продольного положения положения центра тяжести. Более подробный раздел расчета по этому вопросу см. в разделе «Как рассчитать положение центра тяжести». Более простой расчет можно увидеть ниже:
И:
Где:
- b = Расстояние от центра тяжести до задних колес (м)
- Wf = масса переднего моста (кг)
- Вес = общая масса автомобиля (кг)
- L = Колесная база (м)
- a = Положение центра тяжести Расстояние от передних колес (м)
Следовательно:
И:
В этом примере автомобиль симметричен, поэтому положение центра тяжести лежит на центральной линии ширины колеи автомобиля.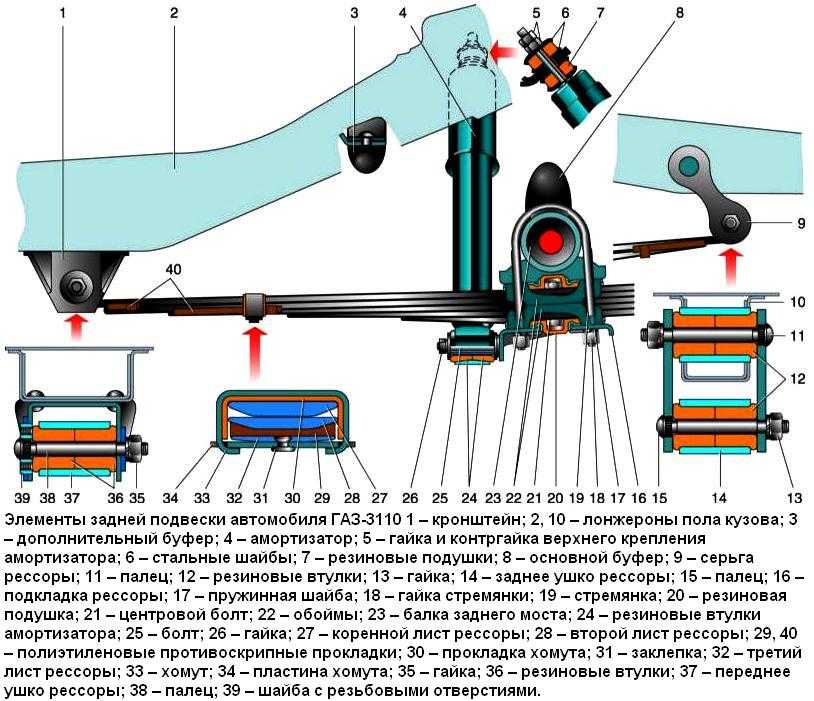 Теперь значения поперечного ускорения можно рассчитать относительно углов пути и земли. Если вы участвуете в гонках по наклонной или плоской трассе, значения здесь будут отличаться. Поэтому мы выполнили этот следующий раздел дважды. Сначала мы использовали цифры для разворота с креном, встречающиеся в таких ситуациях, как NASCAR. Затем мы выполнили те же расчеты настройки для автомобиля на ровной трассе, такой как Сильверстоун. Просто используйте тот раздел, который применим к вашему типу вождения.
Теперь значения поперечного ускорения можно рассчитать относительно углов пути и земли. Если вы участвуете в гонках по наклонной или плоской трассе, значения здесь будут отличаться. Поэтому мы выполнили этот следующий раздел дважды. Сначала мы использовали цифры для разворота с креном, встречающиеся в таких ситуациях, как NASCAR. Затем мы выполнили те же расчеты настройки для автомобиля на ровной трассе, такой как Сильверстоун. Просто используйте тот раздел, который применим к вашему типу вождения.
Наклонный контур
Для нашего примера навернутого контура мы будем использовать угол крена (α) равный 9,2 градуса для наших расчетов. Это угол крена на гоночной трассе Indianapolis Motor Speedway, используемой в автомобильных гонках NASCAR и INDY.
А:
А:
Где:
- Aα = горизонтальное боковое ускорение (g)
- Ay = боковое ускорение (g)
- V = скорость прохождения поворотов (м/с)
- R = Угловой радиус (м)
- г = сила тяжести (м/с²)
- α = угол крена (градусы)
- W’ = эффективный вес автомобиля из-за крена (кг)
- Вт = общая статическая масса автомобиля (кг)
Следовательно, используя наши значения из первого раздела, мы можем выполнить следующие вычисления:
И:
И:
Теперь мы можем вернуться к основному разделу расчета. Если вы использовали этот раздел виража, то пропустите следующую часть для расчета значений ускорения на плоской трассе.
Если вы использовали этот раздел виража, то пропустите следующую часть для расчета значений ускорения на плоской трассе.
Плоский контур
Мы можем использовать уравнения, используемые для включения кулисного контура, для расчета ускорения и скоростей передачи нагрузки в плоском контуре. Поскольку наш угол крена (α) равен 0 градусов, мы можем просто заменить следующие значения в уравнениях, чтобы получить целое число:
- Cosα =1
- Sinα = 0
Используя эти два обозначения, мы можем составить следующие уравнения:
А:
А:
Где:
- Aα = горизонтальное боковое ускорение (g)
- Ay = боковое ускорение (g)
- V = скорость прохождения поворотов (м/с)
- R = Угловой радиус (м)
- г = сила тяжести (м/с²)
- α = Угол крена (в данном случае 0 градусов)
- W’ = эффективный вес автомобиля из-за крена (кг)
- Вт = общая статическая масса автомобиля (кг)
Следовательно, используя наши значения из первого раздела, мы можем выполнить следующие вычисления:
И:
И:
Как видите, эффективный вес из-за крена такой же, как вес автомобиля из-за отсутствия крена. Однако теперь у нас есть значения ускорения для последующего использования.
Однако теперь у нас есть значения ускорения для последующего использования.
Возобновление основных расчетов
Теперь мы можем рассчитать эффективные нагрузки на переднюю и заднюю ось из-за прохождения поворотов. В нашем примере по-прежнему будут использоваться значения для плоской цепи, поскольку они применимы к большинству транспортных средств в автоспорте. Однако, если вы следуете этому, чтобы настроить овальный гоночный автомобиль, используйте значения из раздела схемы с креном.
Эффективная нагрузка на переднюю и заднюю оси:
И:
Где:
- W’F= Эффективная масса передней оси (кг)
- W’R = Эффективная масса заднего моста (кг)
- W’ = общая эффективная масса (кг)
- b = Положение центра тяжести Расстояние от задних колес (м)
- L = Колесная база (м)
- a = Положение центра тяжести Расстояние от передних колес (м)
Следовательно, используя наши значения сверху:
И:
Теперь нам нужно рассчитать градиент крена, используя уравнение:
Где:
- Ѳ = угол крена кузова (градусы)
- Ay = боковое ускорение (g)
- W = общая масса автомобиля (кг)
- H = Расстояние от центра тяжести до оси крена (м)
- KθF = Скорость переднего крена (Нм/радиан)
- KθR = Скорость заднего крена (Нм/радиан)
Следовательно:
Теперь мы вычисляем переднюю и заднюю скорости передачи поперечной нагрузки из-за поперечного ускорения. Уравнения для этого:
Уравнения для этого:
И:
Где:
- Wf = передача поперечной нагрузки спереди (кг)
- Wr = передача поперечной нагрузки сзади (кг)
- Ay = боковое ускорение (g)
- W = общая масса автомобиля (кг)
- tf = Ширина передней гусеницы (м)
- tr = Ширина задней гусеницы (м)
- H = Высота центра тяжести от оси крена (м)
- Kθf = Скорость переднего крена (радиан/г)
- Kθr = скорость заднего крена (радиан/г)
- b = Положение центра тяжести Расстояние от задних колес (м)
- L = Колесная база (м)
- a = Положение центра тяжести Расстояние от передних колес (м)
- Zrf = Высота центра переднего валка (м)
- Zrr = высота заднего центра крена (м)
Таким образом, мы можем использовать все наши цифры сверху, чтобы заполнить уравнения и получить ответы:
И:
Из-за того, что величина (Aαcosα) больше, чем (sina) нагрузка на внешнее колесо этого автомобиль увеличится, а нагрузка на внутренние колеса уменьшится по массе; это нормальный способ, которым автомобиль загружает и разгружает колеса во время поворота. Следовательно, мы можем рассчитать отдельные нагрузки на колеса нашего автомобиля, проезжающего этот угол.
Следовательно, мы можем рассчитать отдельные нагрузки на колеса нашего автомобиля, проезжающего этот угол.
- Переднее внешнее колесо = W(fo) = W1+Wf = 460+226,6 = 686,6 кг
- Переднее внутреннее колесо = W(fi) = W2-Wf = 460-226,6 = 233,4 кг
- Заднее внешнее колесо = W(ro) = W3 + Wr = 310+161,87 = 471,87 кг
- Заднее внутреннее колесо = W(ri) = W4 – Wr = 310-161,87 = 148,13 кг
Если какое-либо из приведенных выше конечных значений отрицательное или равно нулю. Это означает, что вы отрываете это колесо от земли. Теперь, когда у нас есть нагрузки на шины для каждого колеса, мы также можем рассчитать изменение нагрузки на шину от статической нагрузки для каждого колеса:
- Замена переднего внешнего колеса = ΔW(fo) = W(fo)-W1 =686,6 – 460= +226,6 кг
- Замена переднего внутреннего колеса = ΔW(fi) =W(fi)-W2 =233,4 – 460= -226,6 кг
- Замена заднего внешнего колеса = ΔW(ro) = W(ro)-W3 = 471,87 – 310= +161,87 кг
- Замена заднего внутреннего колеса = ΔW(ri) =W(ri)-W4 = 148,13 – 310 = -161,87 кг
Вы можете заметить, что приведенные выше значения совпадают с рассчитанными для эффективных колесных нагрузок. Однако цифры были бы другими, если бы использовался пример с наклонным углом.
Однако цифры были бы другими, если бы использовался пример с наклонным углом.
После создания нагрузки на колеса следующим этапом является выбор скоростей движения для жесткости наших пружин, которые были бы достаточно жесткими, чтобы наша внешняя подвеска не прогибалась и не контактировала с отбойниками. Поэтому, если вы рассчитали ранее, что у вас есть 90 мм хода неровностей, то, возможно, стоит использовать 70 мм, чтобы позволить 20 мм учитывать дополнительные непредвиденные силы сжатия, такие как торможение, ускорение, неровности на трассе и т. д. Очень важно избегать дна. извлеките колесо или амортизатор, так как это вызовет внезапное быстрое изменение нагрузки на колесо, так как жесткость пружины станет неэффективной, если в системе есть механическая блокировка. На практике для решения этой проблемы можно использовать отбойники и пружины с нелинейной скоростью нарастания, но чтобы уравнения оставались управляемыми, мы будем предполагать, что отбойники недоступны и что используются полностью линейные пружины.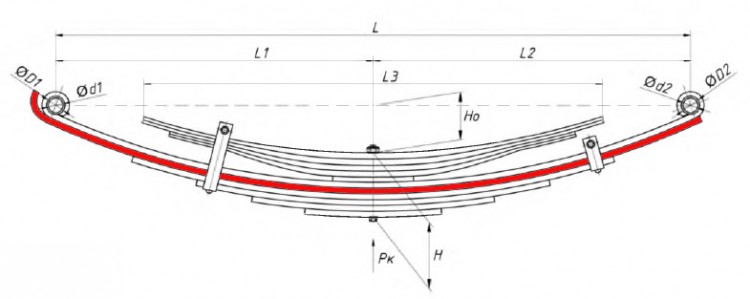
Если у вас есть автомобиль с достаточным дорожным просветом, то основная проблема будет заключаться в том, что амортизатор прогибается при сжатии и контактирует с отбойниками. Если автомобиль является автомобилем с эффектом земли или используется на трассе с креном на скорости, или и то, и другое, то основной проблемой может быть шасси, упирающееся в землю. Выберите наиболее подходящий сценарий и решите, сколько разрешено перемещений по ухабам. В этом примере мы будем использовать значение 70 мм.
Используя наши нагрузки на внешние колеса сверху и допустимый ход неровностей, мы можем рассчитать требуемую скорость движения спереди и сзади:
И:
Где:
- Krf = Передняя скорость (Н/м)
- Krr = Скорость заднего хода (Н/м)
- x1 = припуск на передний неровность (м)
- x2 = припуск на задний бампер (м)
Следовательно:
И:
Теперь мы можем рассчитать частоты поездок, продолжая предполагать поперечную симметрию.
И:
Чтобы преобразовать эти частоты поездок в циклы в минуту, просто умножьте их на 60, чтобы получить:
- ωf = 1,32 Гц X 60 = 79,2 имп/мин
- ωr = 1,36 Гц X 60 = 81,6 импульсов в минуту
В этом примере мы рассматриваем заднеприводный гоночный автомобиль с передним расположением двигателя. Из опыта и данных автоспорта мы знаем, что собственная частота передних колес обычно выше, чем у задних. В приведенных выше расчетах это не так. Следовательно, мы можем сказать, что собственная частота фронта должна быть выше 81,6 имп/мин и, следовательно, будет увеличена до 86 имп/мин при первом проходе расчета. Если у вас переднеприводная машина, собственная частота задних колес должна быть выше, чем передних. Если это не так, то вы должны сделать процесс, аналогичный приведенному ниже, но увеличить собственную частоту заднего, а не переднего.
Чтобы увеличить собственную частоту фронта, мы можем возвести в квадрат отношение двух собственных частот. Используя приведенное ниже уравнение:
Используя приведенное ниже уравнение:
Используя это отношение, новая передняя скорость движения равна:
Чтобы убедиться, что наша новая передняя скорость движения имеет более высокую собственную частоту, чем задняя, мы можем повторно запустить уравнение передней собственной частоты. с нашей новой скоростью движения вперед, как показано ниже:
Новый ответ для нашей собственной частоты фронта достаточно близок к нашему приближению, чтобы продолжить с этими значениями. После того, как наш первый запуск расчетов скорости езды завершен, мы теперь можем использовать эти значения скорости пружины и сравнить их с скоростью вращения, которая была принята в начале процесса, чтобы увидеть, насколько мы близки. Предполагая симметрию и то, что мы хотим, чтобы скорости движения слева и справа были одинаковыми, расчеты скоростей крена спереди и сзади:
And:
Эти значения для крена намного ниже наших предполагаемых скоростей крена в начале:
- Передняя скорость крена = 94900 Нм/рад
- Скорость заднего крена = 67800 Нм/рад
Таким образом, разница между этими значениями является требуемой жесткостью пружины стабилизатора поперечной устойчивости для наших передней и задней осей. Поэтому можно сказать, что на наши переднюю и заднюю оси можно установить стабилизатор поперечной устойчивости. Требуемые жесткости пружины стабилизатора поперечной устойчивости на данный момент будут:
Поэтому можно сказать, что на наши переднюю и заднюю оси можно установить стабилизатор поперечной устойчивости. Требуемые жесткости пружины стабилизатора поперечной устойчивости на данный момент будут:
And
Если вы не можете установить дугу безопасности на свой автомобиль с одной стороны, вам следует продолжить приведенные ниже несколько уравнений, просто используя скорость вращения винтовой пружины для этого конца, чтобы увидеть, какое влияние она оказывает на колесо. смещение. Из соображений интереса, если у вас не было автомобиля с поперечной симметрией скорости движения, такого как овальный гоночный автомобиль, то для определения скорости крена спереди и сзади можно использовать приведенное ниже уравнение:
Теперь мы можем повторить запустим некоторые уравнения из предыдущих, чтобы проверить, что смещения нашего колеса соответствуют желаемым. Прежде всего, мы должны повторно запустить наше уравнение градиента качения, полученное ранее, со всеми 4 значениями жесткости качения:
Если вы хотите преобразовать свой ответ в градусы на г, чтобы сравнить ваш результат с более ранними классифицированными значениями, то можно использовать приведенную ниже формулу преобразования.
Таким образом, наш ответ:
Глядя на начало процесса, где мы показали примеры градиентов крена, это относится к жесткому концу высокопроизводительных дорожных и трековых автомобилей и находится за пределами категории специально построенных гоночных автомобилей. . Это идеально подходит для нашего примера, поэтому мы пока продолжим с этим значением, так как значение снова немного изменится к концу процесса.
И если предположить, что высота центра крена не изменилась, наши коэффициенты переноса веса на переднее и заднее колеса составляют:
И:
И наши нагрузки на внешние колеса составляют:
- Переднее внешнее колесо = W(fo) = W1 +Wf = 460+226,6 = 686,6 кг
- Заднее внешнее колесо = W(ro) = W3 + Wr = 310+161,87 = 471,87 кг
И наши изменения от статических нагрузок на колеса для наших внешних колес:
- Изменение переднего внешнего колеса = ΔW(fo) = W(fo)-W1 =686,6 – 460= +226,6 кг
- Замена заднего внешнего колеса = ΔW(ro) = W(ro)-W3 = 471,87 – 310= +161,87 кг
Таким образом, наш рабочий объем колес составляет:
И
Наш рабочий объем передних колес близок к тому, что мы изначально хотели от нашей машины, но немного меньше. Это достаточно близко, чтобы принять значение скорости переднего хода для нашего примера. Объем заднего колеса точно такой же, поэтому мы можем использовать эти цифры для оценки скорости движения, чтобы двигаться вперед в наших расчетах. Если вы приводили цифры, например, где вы не смогли установить стабилизатор поперечной устойчивости, то ваши ответы о нагрузках на колеса и смещении колес могли измениться.
Это достаточно близко, чтобы принять значение скорости переднего хода для нашего примера. Объем заднего колеса точно такой же, поэтому мы можем использовать эти цифры для оценки скорости движения, чтобы двигаться вперед в наших расчетах. Если вы приводили цифры, например, где вы не смогли установить стабилизатор поперечной устойчивости, то ваши ответы о нагрузках на колеса и смещении колес могли измениться.
Это хороший момент, чтобы проверить значение градиента крена и значение частоты поездок с цифрами в начале статьи, чтобы убедиться, что ваши значения относятся к правильной категории автомобиля. Если он близок к вашей категории, например, скоростной автомобиль, который близок к гоночному автомобилю, оставьте свои значения. Однако, если один или оба ваших ответа помещают вас в группу легковых автомобилей, когда вы стремитесь построить гоночный автомобиль, вам нужно будет изменить свои первоначальные предположения в начале и повторно запустить уравнения.
Кроме того, если вы не были удовлетворены своими ответами на этом этапе, вы можете вернуться к разделу определения ограничений хода колес или, если они фиксированы, вы можете изменить такие элементы, как высота центра крена и ширина колеи, которые изменят более ранние расчеты и не действуют до этого момента.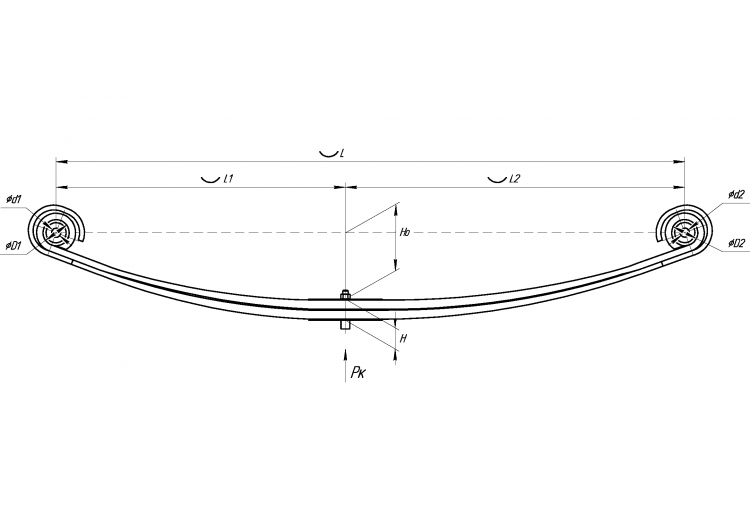

 На каком расстоянии от него ударила молния? Скорость звука в воздухе 340 м/с.
На каком расстоянии от него ударила молния? Скорость звука в воздухе 340 м/с.
 Чему равна длина волны?
Чему равна длина волны?

 Скорость звука в воздухе 340 м/с.
Скорость звука в воздухе 340 м/с. На каком расстоянии от наблюдателя произошёл грозовой разряд?
На каком расстоянии от наблюдателя произошёл грозовой разряд?
 Полная энергия равна 0,6 Дж. На расстоянии 3 см от положения равновесия упругая сила, действующая на шарик со стороны пружины, равна 10 Н. Определите амплитуду колебаний.
Полная энергия равна 0,6 Дж. На расстоянии 3 см от положения равновесия упругая сила, действующая на шарик со стороны пружины, равна 10 Н. Определите амплитуду колебаний.
Добавить комментарий